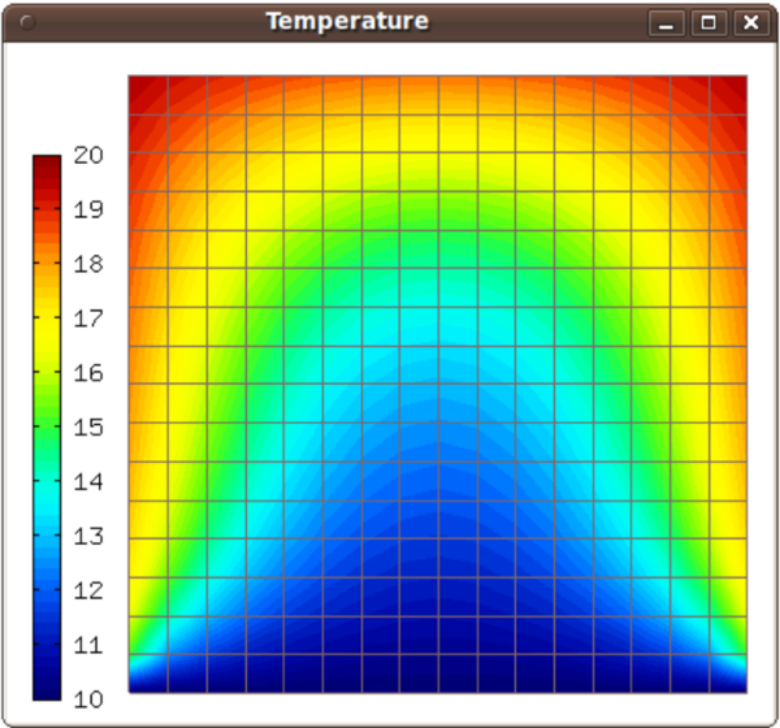
Trilinos - Timedep (03-trilinos-timedep)

This example shows how to use Trilinos for time-dependent PDE problems. The NOX solver is employed, either using Newton’s method or JFNK, and with or without preconditioning,

Model problem

We solve a linear heat transfer equation

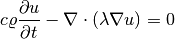
in a square domain where a Dirichlet boundary condition is prescribed on the bottom edge and the rest of the boundary has a Newton boundary condition

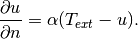
Here is heat capacity, material density, 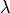thermal conductivity of the material, 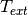exterior temperature, and 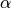heat transfer coefficient.

Time stepping

The initial coefficient vector has to be provided to NOX in each time step. The time stepping loop is as follows:

// Time stepping loop:
double total_time = 0.0;
for (int ts = 1; total_time <= 2000.0; ts++)
{
  info("---- Time step %d, t = %g s", ts, total_time += TAU);

  info("Assembling by DiscreteProblem, solving by NOX.");
  solver.set_init_sln(coeff_vec);
  if (solver.solve())
    Solution::vector_to_solution(solver.get_solution(), &space, &t_prev_time);
  else
    error("NOX failed.");

  // Show the new solution.
  Tview.show(&t_prev_time);

  info("Number of nonlin iterations: %d (norm of residual: %g)",
    solver.get_num_iters(), solver.get_residual());
  info("Total number of iterations in linsolver: %d (achieved tolerance in the last step: %g)",
    solver.get_num_lin_iters(), solver.get_achieved_tol());
}

Sample results

You should see the following result: