Nonlinear Example (03-nonlinear)

Model problem

Showing a nonlinear time-dependent problem is not really necessary since linear and nonlinear problems are treated in the same way. But let us show one anyway. Our model problem will be a time-dependent version of the example used in part P02:

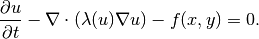
We prescribe nonhomogeneous Dirichlet boundary conditions

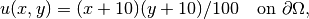
and the same function is used to define the initial condition. The problem will be solved in the square 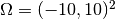and time interval .

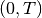Weak formulation

In order to use arbitrary Runge-Kutta methods, the time derivative is put on the left-hand side of the equation and everything else is put on the right:

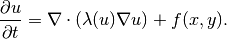
Then the time derivative term is skipped and we write the weak form for the stationary residual (right-hand side) only:

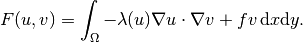
Weak forms

After inverting the sign of the custom nonlinearity,

double CustomNonlinearity::value(double u) const
{
  return -1 - Hermes::pow(u, alpha);
}

the DefaultWeakFormPoisson can be used:

// Initialize the weak formulation
CustomNonlinearity lambda(alpha);
Hermes2DFunction<double> f(heat_src);
DefaultWeakFormPoisson<double> wf(HERMES_ANY, &lambda, &f);

Time stepping loop

The time stepping loop is analogous to the previous example:

// Time stepping loop:
double current_time = 0; int ts = 1;
do
{
  // Perform one Runge-Kutta time step according to the selected Butcher's table.
  info("Runge-Kutta time step (t = %g s, tau = %g s, stages: %d).",
        current_time, time_step, bt.get_size());

              runge_kutta.set_newton_tol(NEWTON_TOL);
                    runge_kutta.set_newton_max_iter(NEWTON_MAX_ITER);
                    runge_kutta.set_verbose_output(true);
                    runge_kutta.set_newton_damping_coeff(1.0);
                    runge_kutta.set_newton_max_allowed_residual_norm(1e10);

  Hermes::vector<Solution<double>*> slns_time_prev;
  slns_time_prev.push_back(&sln_time_prev);
  Hermes::vector<Solution<double>*> slns_time_new;
  slns_time_new.push_back(&sln_time_new);

                    runge_kutta.setTime(current_time);
  runge_kutta.setTimeStep(time_step);

                    try
                    {
                            runge_kutta.rk_time_step_newton(slns_time_prev, slns_time_new);
                    }
                    catch(Exceptions::Exception& e)
                    {
                            std::cout << e.what();
                    }

  // Update time.
  current_time += time_step;

  // Show the new time level solution.
  char title[100];
  sprintf(title, "Solution, t = %g", current_time);
  sview.set_title(title);
  sview.show(&sln_time_new);
  oview.show(&space);

  // Copy solution for the new time step.
  sln_time_prev.copy(&sln_time_new);

  // Increase counter of time steps.
  ts++;
}
while (current_time < T_FINAL);