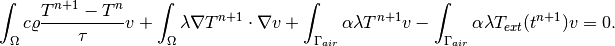Using the Implicit Euler Method (01-implicit-euler)¶
Model problem¶
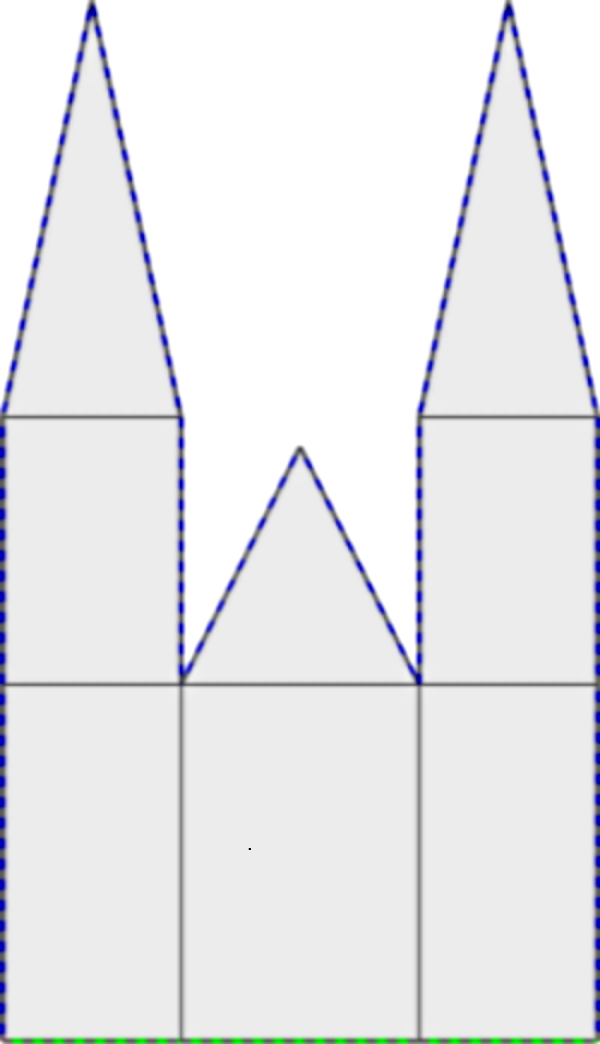
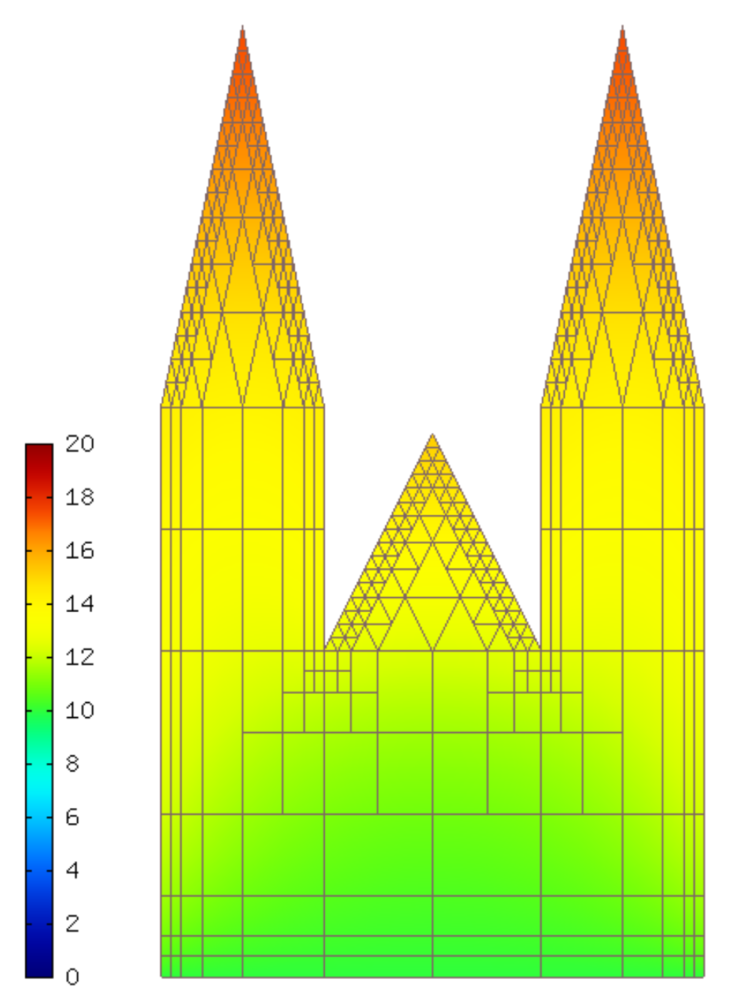
This section describes how a time-integration method can be built into the weak formulation of a PDE (usually this is called Rothe’s method). We will illustrate this on the implicit Euler method applied to a heat transfer equation. The equation describes in a naive approximation how the St. Vitus cathedral in Prague responds to changes in the surrounding air temperature during one 24-hour cycle. The geometry is shown below:
We assume the standard heat transfer equation
(1)
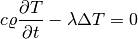
equipped with a Dirichlet condition
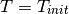
on the bottom edge 
and a Newton condition
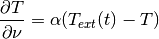
on the rest of the boundary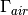 
. Here, 
is the heat capacity of the material,
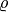the material density, 
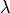the thermal conductivity,
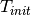the fixed temperature on the
ground (same as the initial temperature of the building), and 
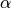the heat transfer coefficient
between the building and the surrounding air. The surrounding air temperature
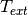is time-dependent of the form
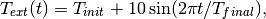
where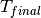 
is 24 hours (translated into seconds).
Equation (1) is equipped with an initial condition of the form
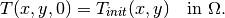
Replacing in (1) the temporal derivative with the backward time difference, we obtain
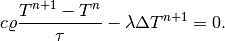
Defining weak forms¶
The weak formulation is a combination of default and custom weak forms, see files definitions.h and definitions.cpp.
Passing and accessing previous time level solution¶
Notice how previous time level solution is passed into the volumetric vector form:
CustomVectorFormVol* vec_form_vol = new CustomVectorFormVol(0, time_step);
vec_form_vol->ext.push_back(prev_time_sln);
add_vector_form(vec_form_vol);
and also how it is accessed from inside the weak form:
Func<double> *temp_prev_time = ext->fn[0];
Keeping the Jacobian if it did not change¶
As this problem is linear, the Jacobian matrix just needs to be constructed once at the beginning, and it will not change during the computation. Thus instead of the usual method NewtonSolver::solve() we use the method NewtonSolver::solve_keep_jacobian():
// This is important in time-dependent examples, these methods are shared by all the 'calculation' classes, i.e. RungeKutta, NewtonSolver, PicardSolver, LinearSolver, DiscreteProblem, DiscreteProblemLinear.
// Perform Newton's iteration.
try
{
newton.solve_keep_jacobian(coeff_vec);
}
catch(Hermes::Exceptions::Exception e)
{
e.printMsg();
}
