NIST-03 (Linear Elasticity)¶
This problem is a coupled system of two equations with a mixed derivative in the coupling term (Lame equations); the context of the problem comes from the subject of linear elasticity.
Model problem¶
Equation solved: Coupled system of two equations
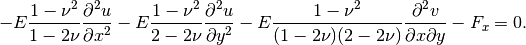
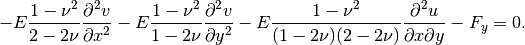
where 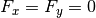 ,
, 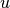 and
and  are the
are the 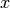 and
and 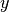 displacements,
displacements, 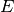 is Young’s Modulus, and
is Young’s Modulus, and 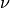 is Poisson’s ratio.
is Poisson’s ratio.
Domain of interest: 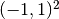 with a slit from
with a slit from 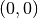 to
to 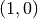 .
.
Boundary conditions: Dirichlet, given by exact solution.
Exact solution¶
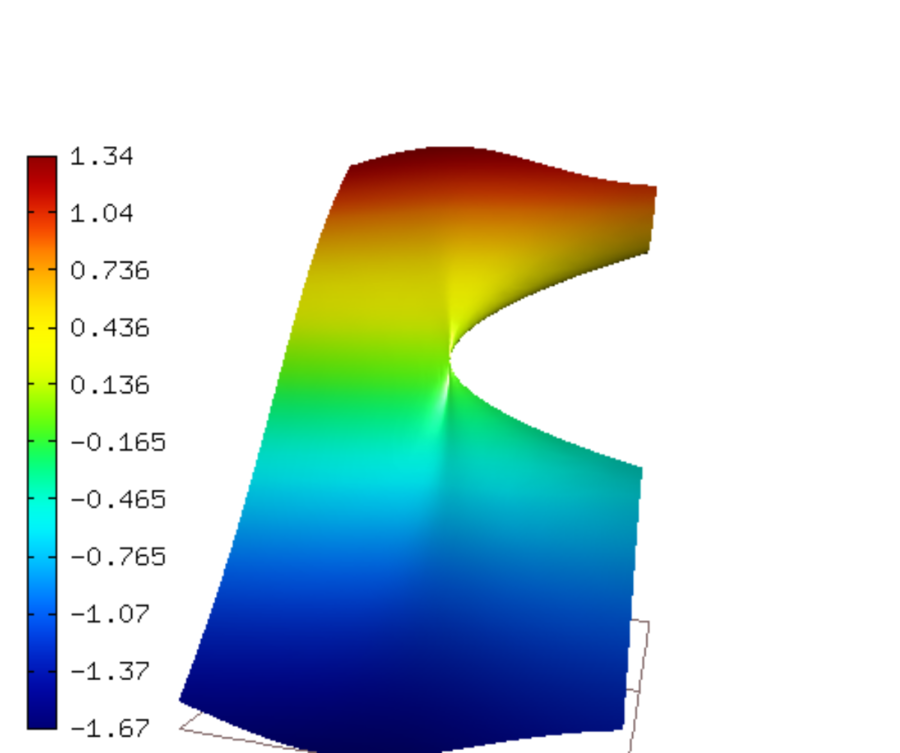
Known exact solution for mode 1:
![u(x, y) = \frac{1}{2G} r^{\lambda}[(k - Q(\lambda + 1))cos(\lambda \theta) - \lambda cos((\lambda - 2) \theta)].](../../../_images/math/b96594289d3c70d65f398b52474de7249b285c55.png)
![v(x, y) = \frac{1}{2G} r^{\lambda}[(k + Q(\lambda + 1))sin(\lambda \theta) + \lambda sin((\lambda - 2) \theta)].](../../../_images/math/68fb2eaced34472ec14890e4a6ab73b4ef690411.png)
here lambda = 0.5444837367825, and Q = 0.5430755788367.
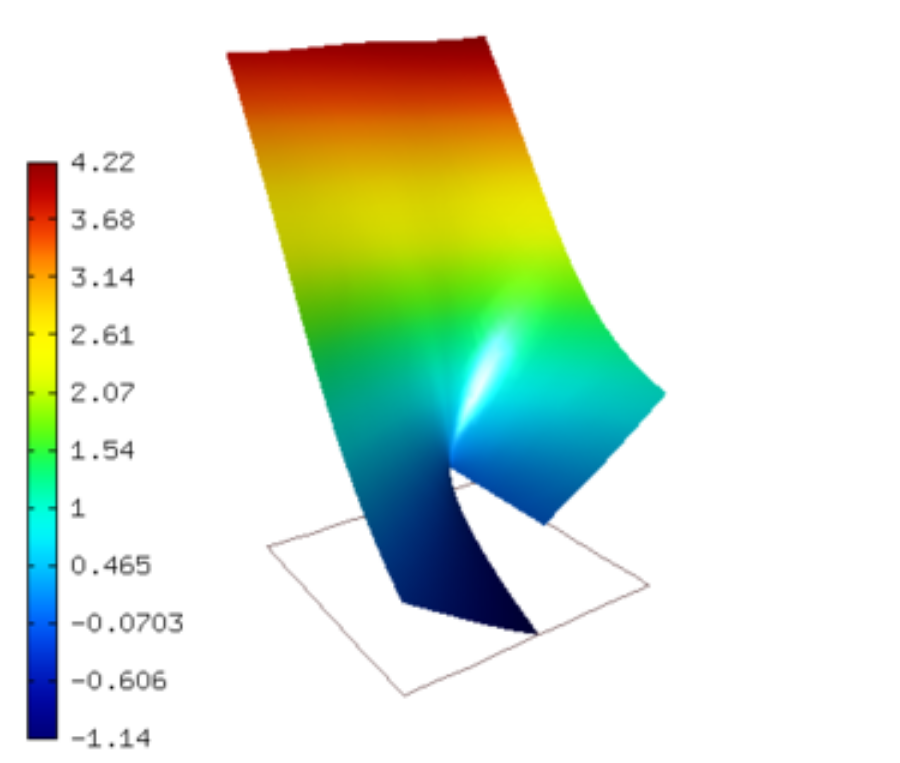
Known exact solution for mode 2:
![u(x, y) = \frac{1}{2G} r^{\lambda}[(k - Q(\lambda + 1))sin(\lambda \theta) - \lambda sin((\lambda - 2) \theta)].](../../../_images/math/766a754d142051ed3520be9b18cd7f5457578801.png)
![v(x, y) = -\frac{1}{2G} r^{\lambda}[(k + Q(\lambda + 1))cos(\lambda \theta) + \lambda cos((\lambda - 2) \theta)].](../../../_images/math/22fd4814acd279c6803bd726013c56f07a43bdfb.png)
here lambda = 0.9085291898461, and Q = -0.2189232362488.
Both in mode 1 and mode 2, 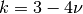 , and
, and 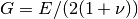 .
.
Comparison of h-FEM (p=1), h-FEM (p=2) and hp-FEM with anisotropic refinements¶
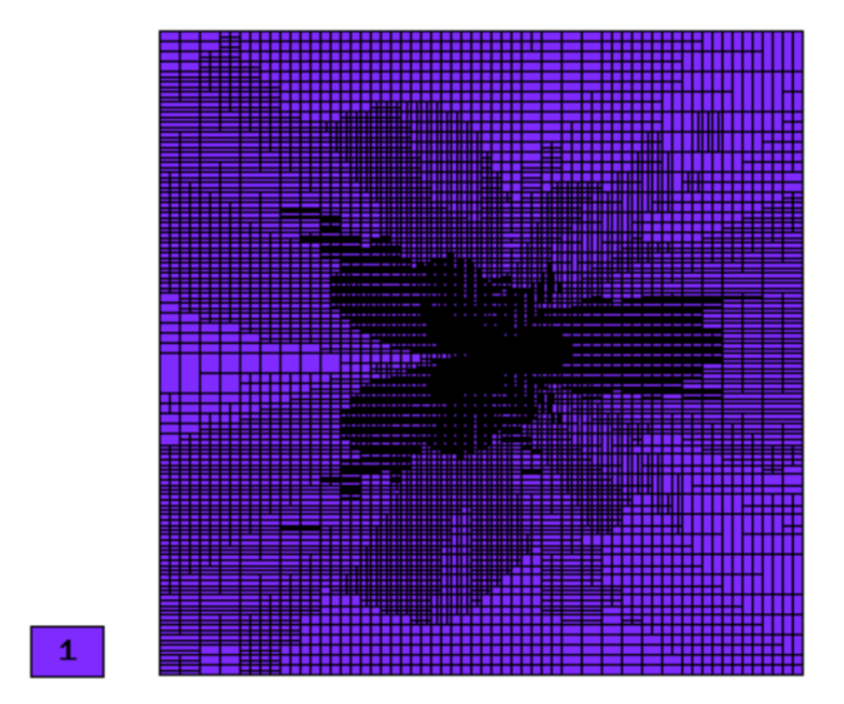
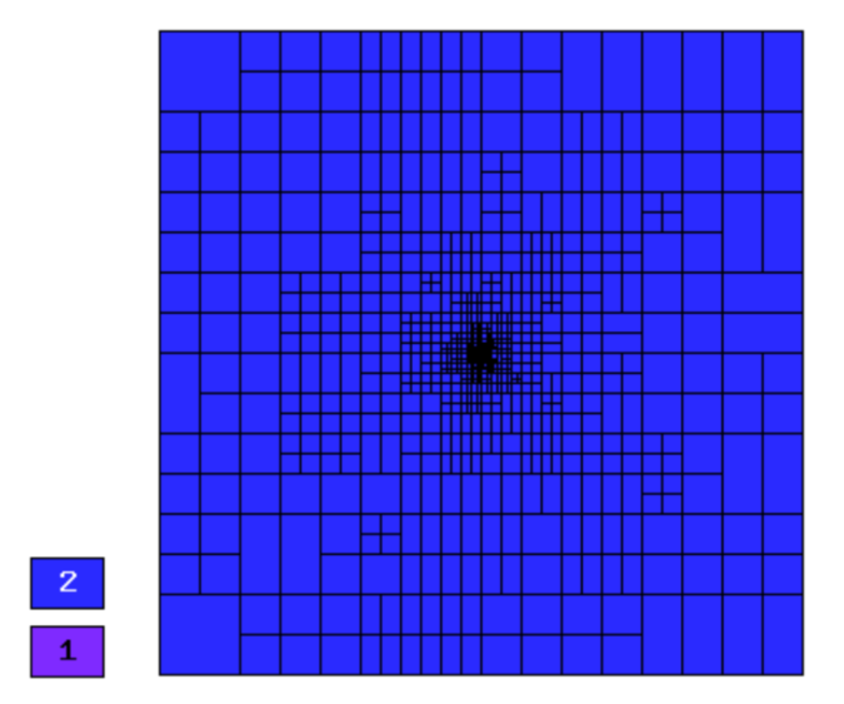
Final mesh (h-FEM, p=1, anisotropic refinements):
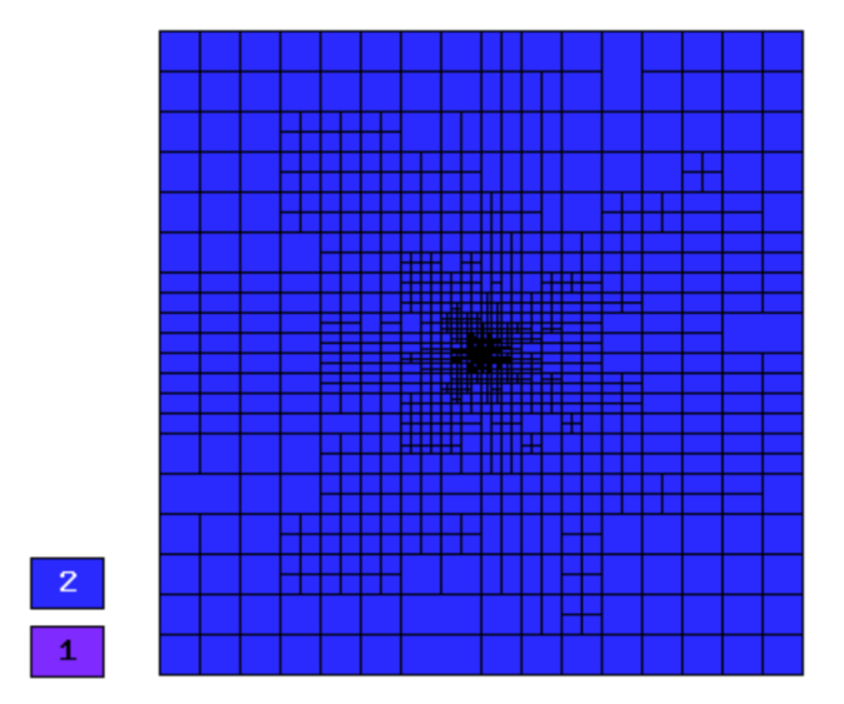
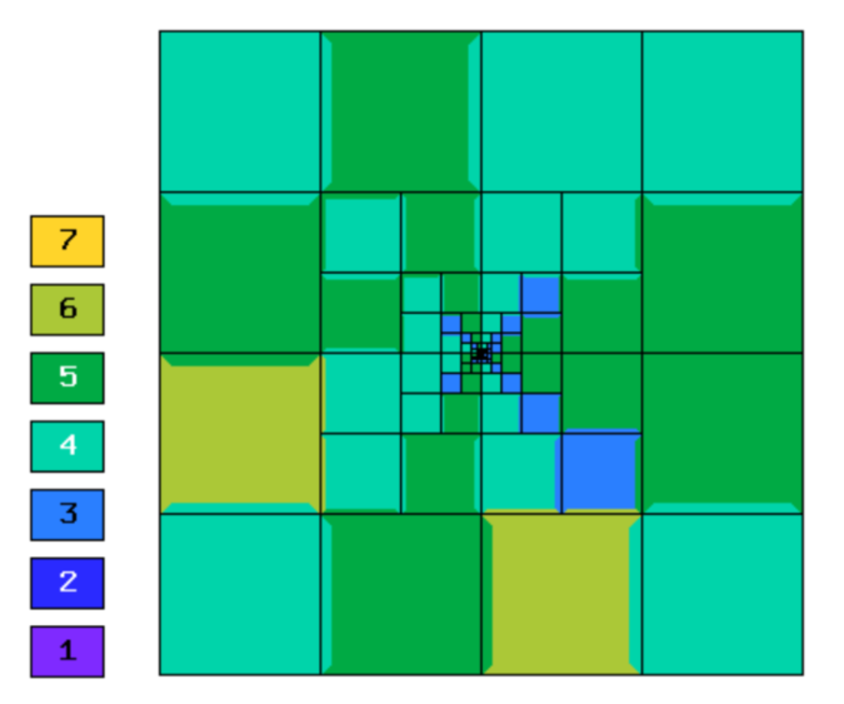
Final mesh (h-FEM, p=2, anisotropic refinements):
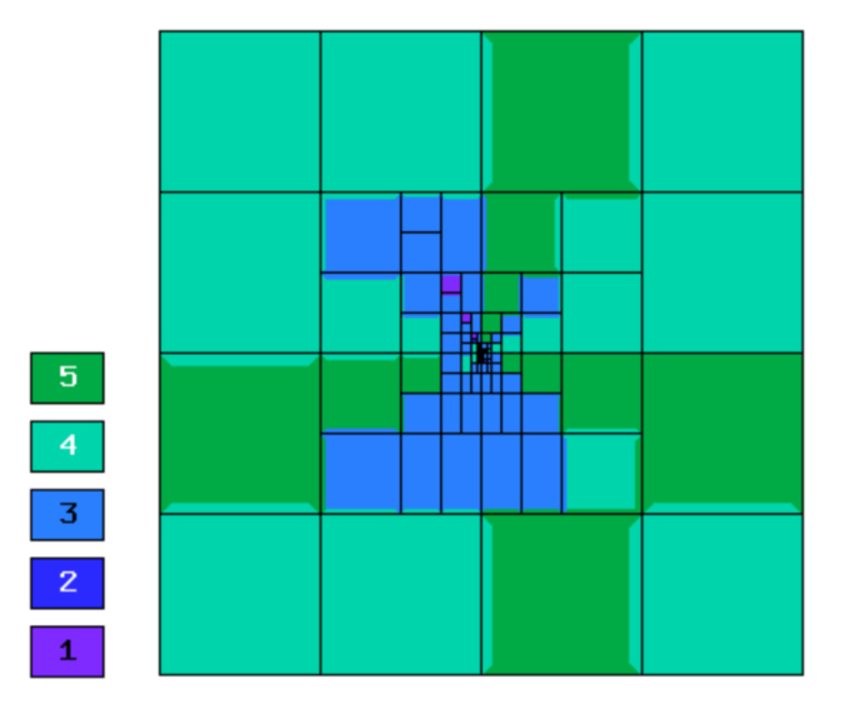
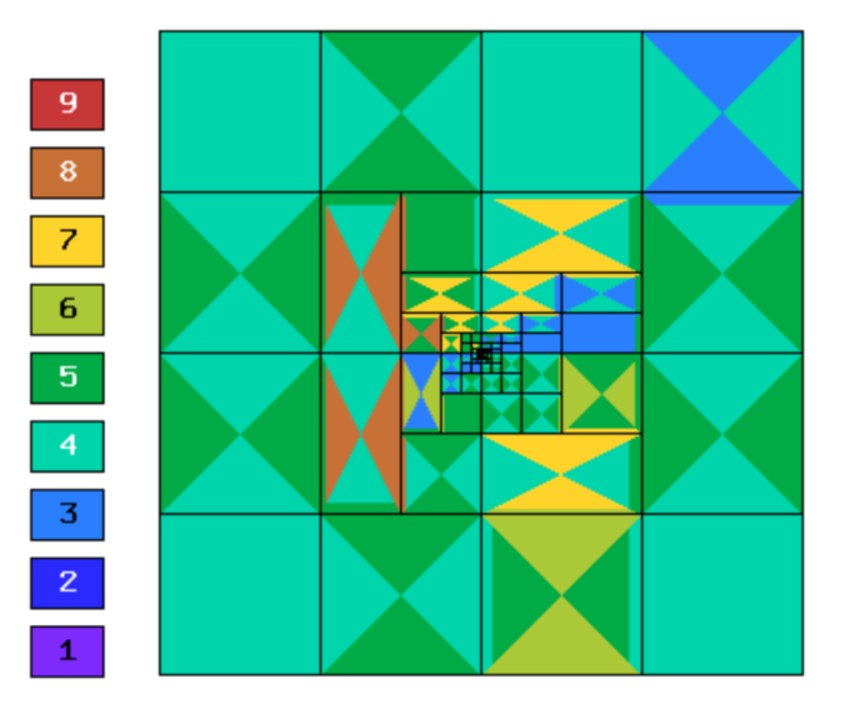
Final mesh (hp-FEM, h-anisotropic refinements):
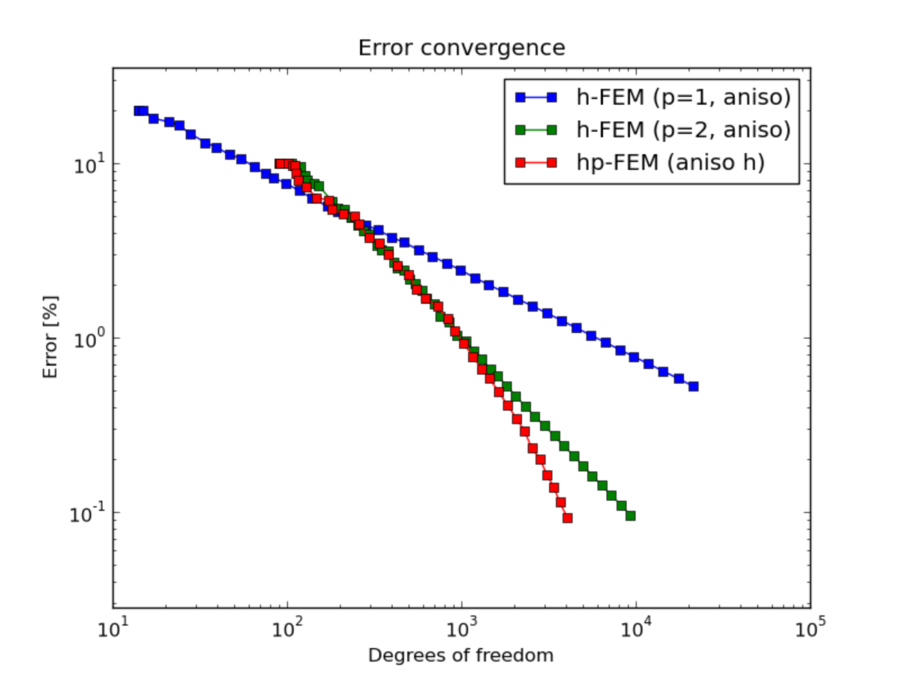
DOF convergence graphs:
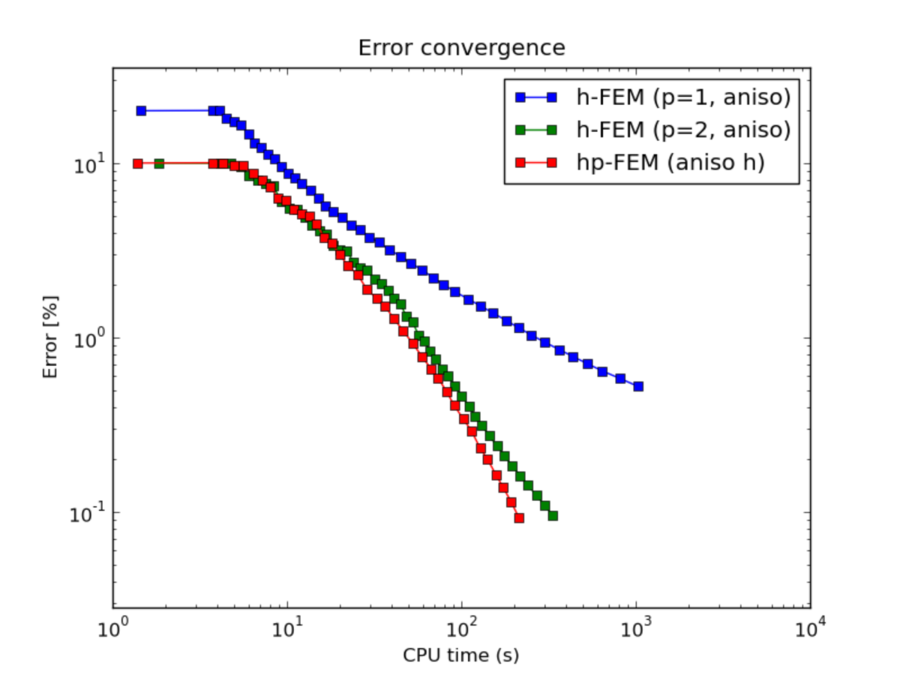
CPU convergence graphs:
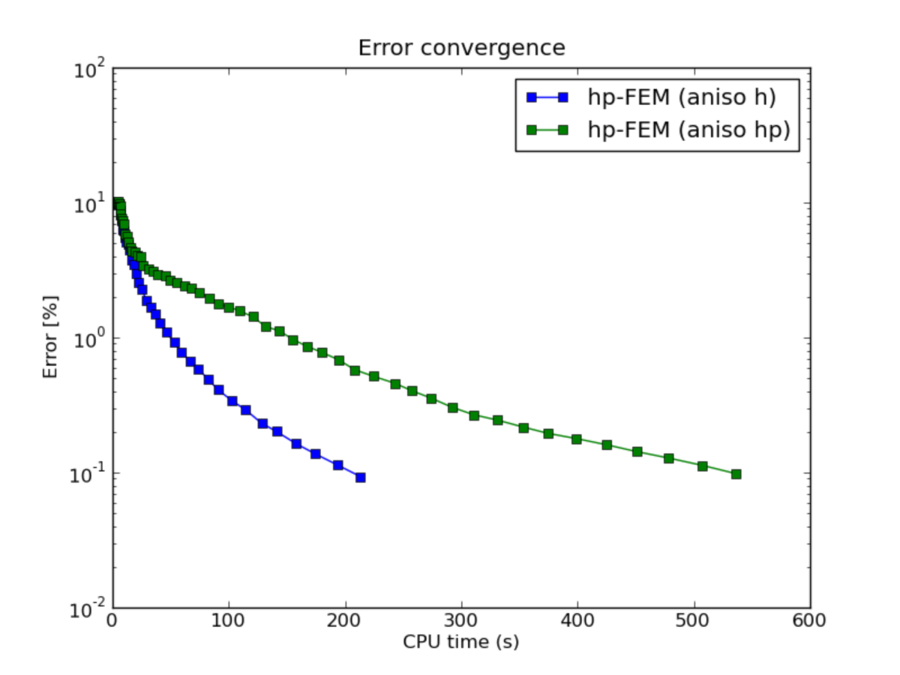
hp-FEM with h-aniso and hp-aniso refinements¶
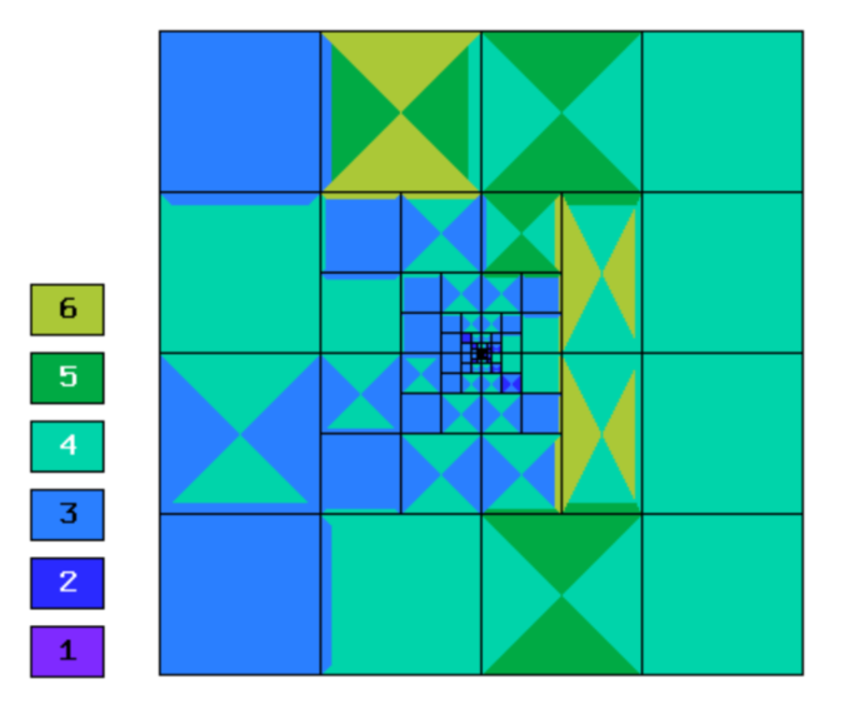
Final mesh (hp-FEM, h-anisotropic refinements):
Final mesh (hp-FEM, hp-anisotropic refinements):
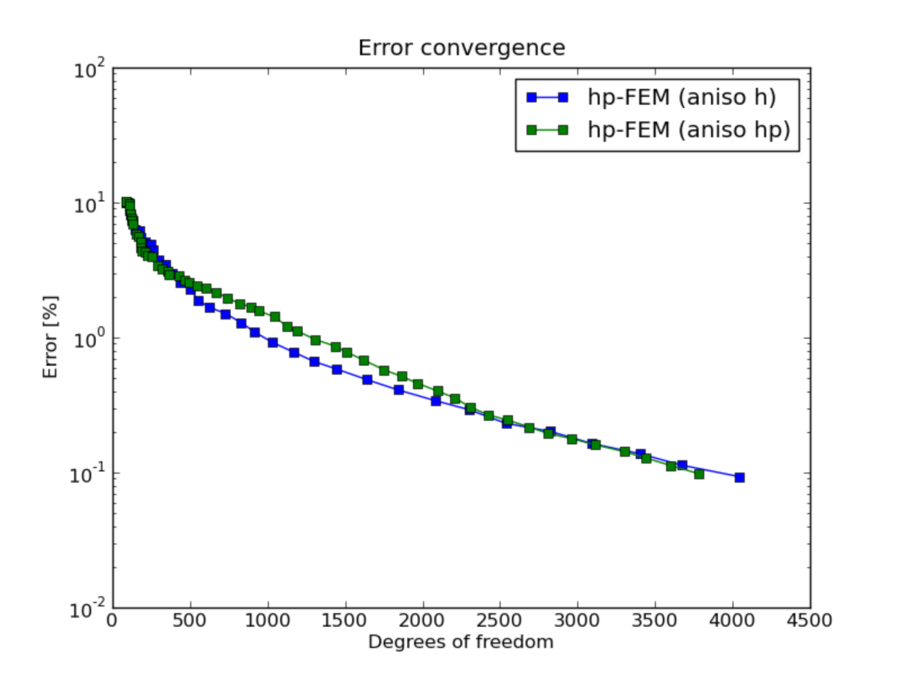
DOF convergence graphs:
CPU convergence graphs: