NIST-09 (Wave Front)¶
Commonly used for testing adaptive refinement algorithms is Poisson’s equation with a solution that has a steep wave front in the interior of the domain.
Model problem¶
Equation solved: Poisson equation
(1)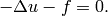
Domain of interest: Unit Square 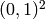
Boundary conditions: Dirichlet, given by exact solution.
Exact solution¶
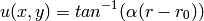
where 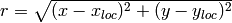 ,
, 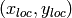 is the center of the circular wave front,
is the center of the circular wave front,
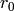 is the distance from the wave front to the center of the circle, and
is the distance from the wave front to the center of the circle, and  gives the steepness of the wave front.
gives the steepness of the wave front.
Material parameters¶
This benchmark has four different versions, we use the global variable PARAM (below) to switch among them.
int PARAM = 3; // PARAM determines which parameter values you wish to use
// for the steepness and location of the wave front.
// | name | ALPHA | X_LOC | Y_LOC | R_ZERO
// 0: mild 20 -0.05 -0.05 0.7
// 1: steep 1000 -0.05 -0.05 0.7
// 2: asymmetric 1000 1.5 0.25 0.92
// 3: well 50 0.5 0.5 0.25
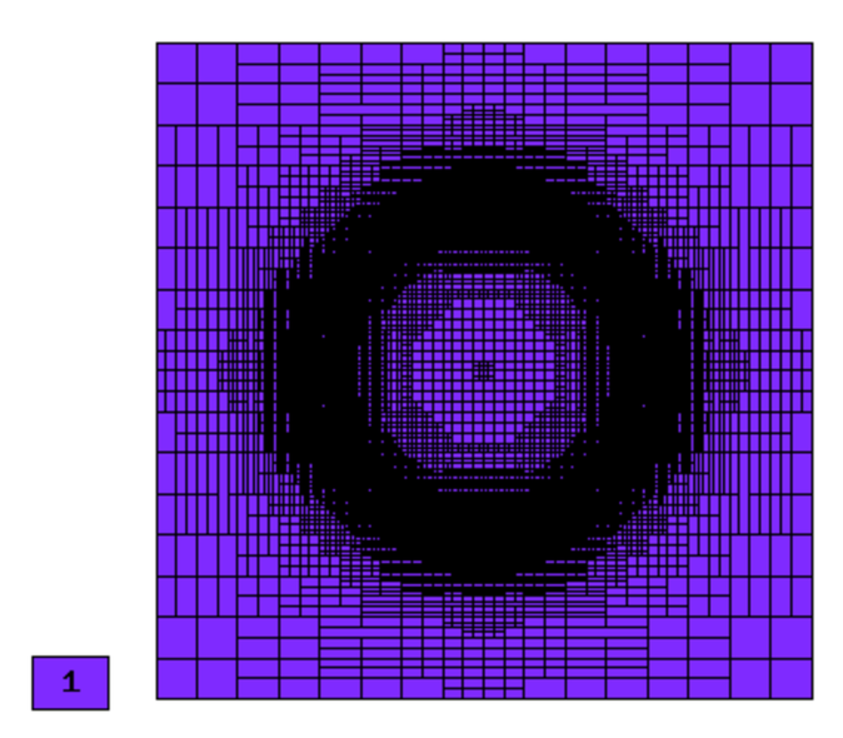
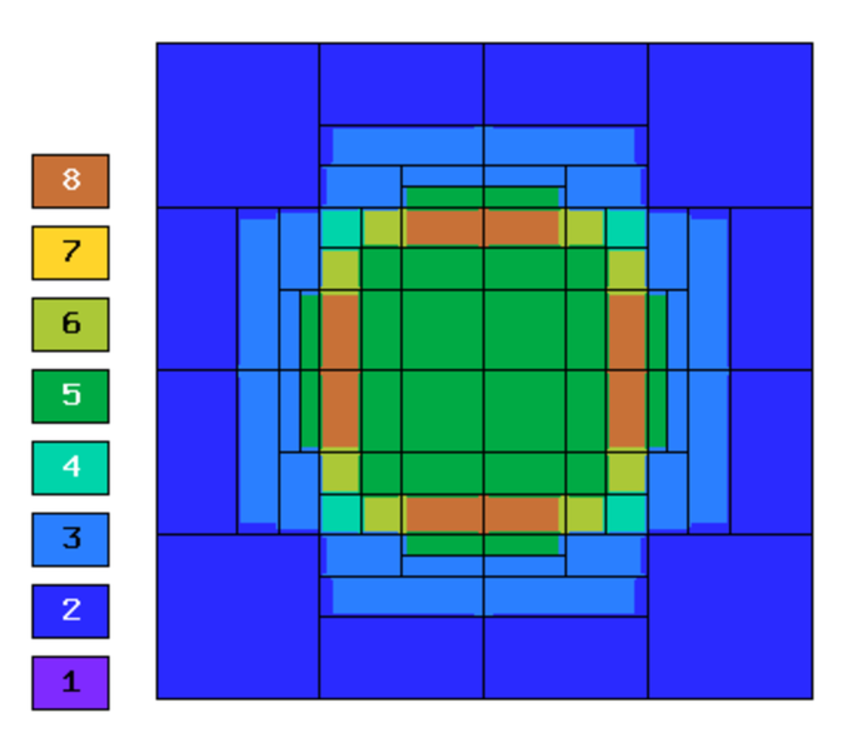
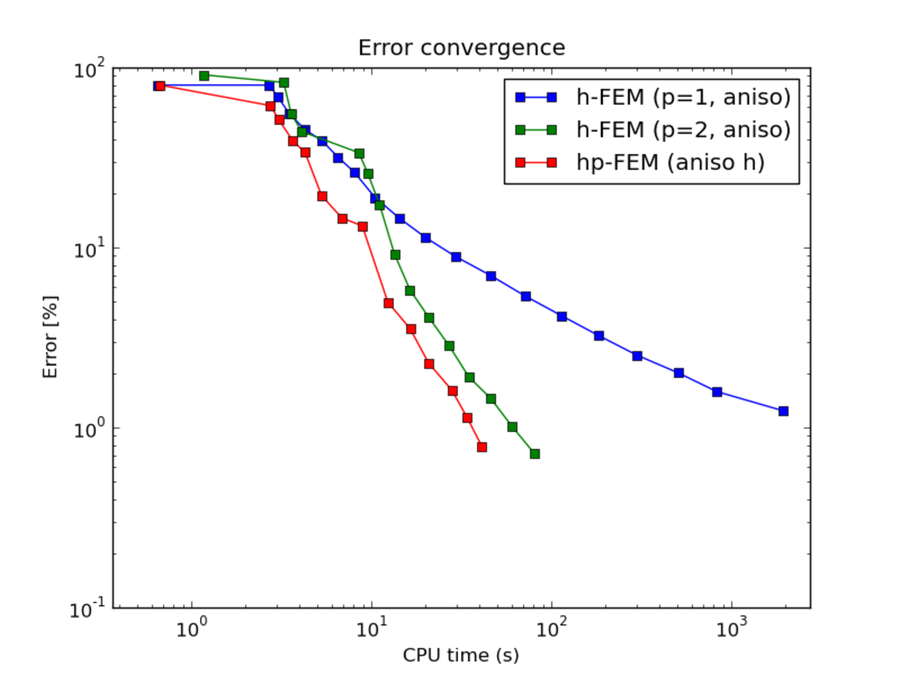
Comparison of h-FEM (p=1), h-FEM (p=2) and hp-FEM with anisotropic refinements¶
Final mesh (h-FEM, p=1, anisotropic refinements):
Final mesh (h-FEM, p=2, anisotropic refinements):
Final mesh (hp-FEM, h-anisotropic refinements):
DOF convergence graphs:
CPU convergence graphs:
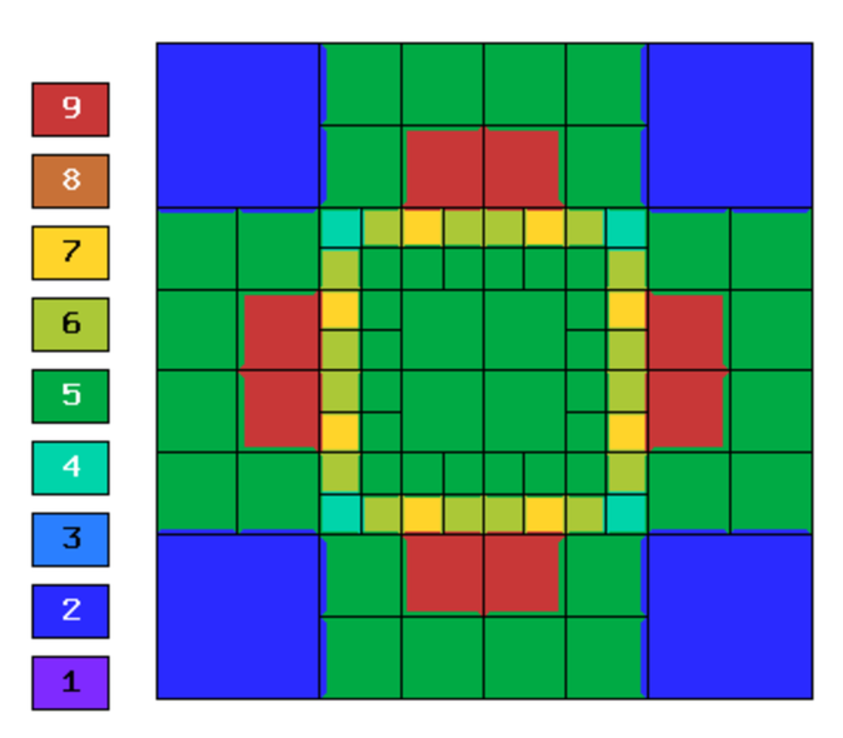
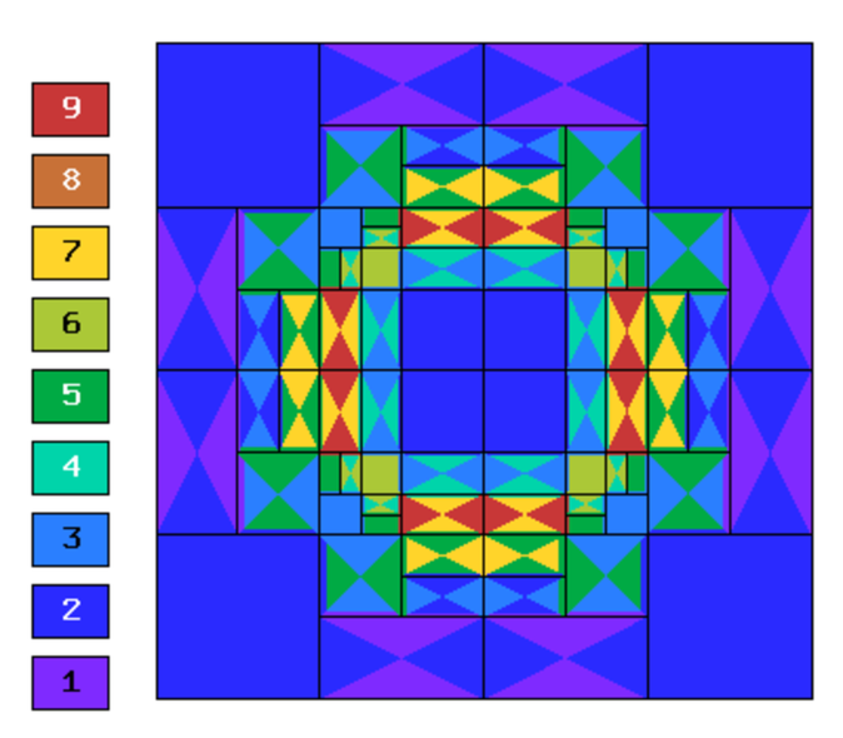
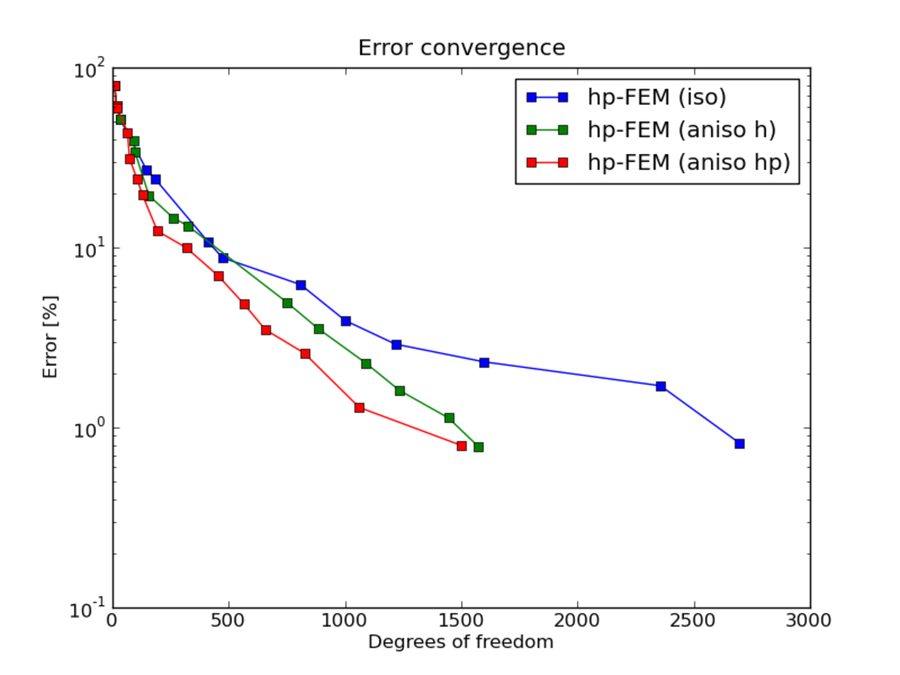
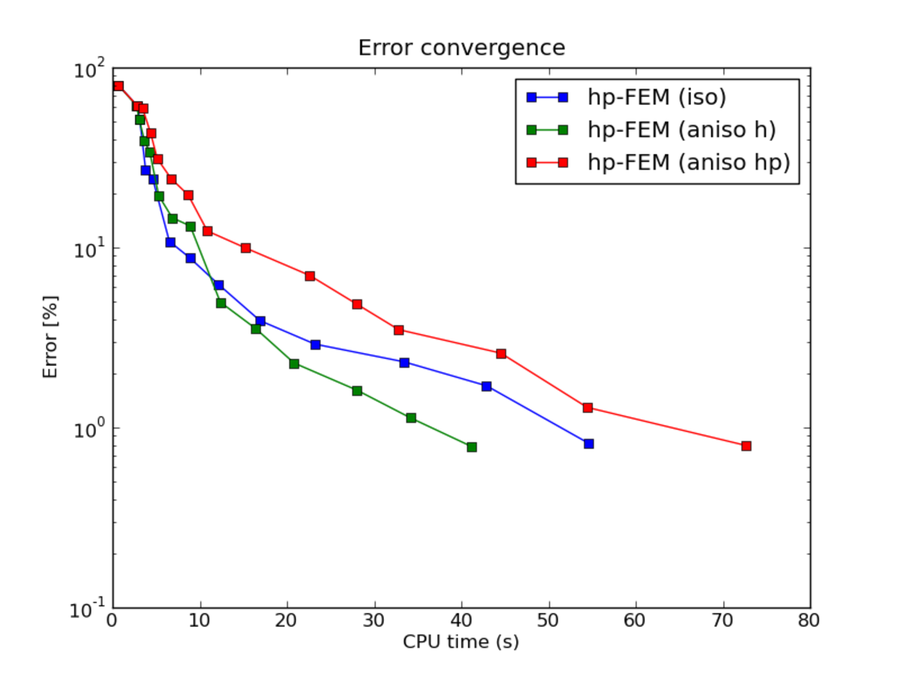
hp-FEM with iso, h-aniso and hp-aniso refinements¶
Final mesh (hp-FEM, isotropic refinements):
Final mesh (hp-FEM, h-anisotropic refinements):
Final mesh (hp-FEM, hp-anisotropic refinements):
DOF convergence graphs:
CPU convergence graphs:
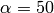 ,
,  , and
, and 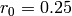 :
: