NIST-08 (Oscillatory)¶
This problem is inspired by the wave function that satisfies a Shrodinger equation model of two interacting atoms. It is highly oscillatory near the origin, with the wavelength decreasing closer to the origin.
Model problem¶
Equation solved: Hemholtz equation
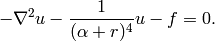
where  . The number of oscillations,
. The number of oscillations, 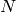 , is determined by the parameter
, is determined by the parameter 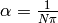
Domain of interest: Unit Square  .
.
Boundary conditions: Dirichlet, given by exact solution.
Exact solution¶

Right-hand side¶
Obtained by inserting the exact solution into the equation.
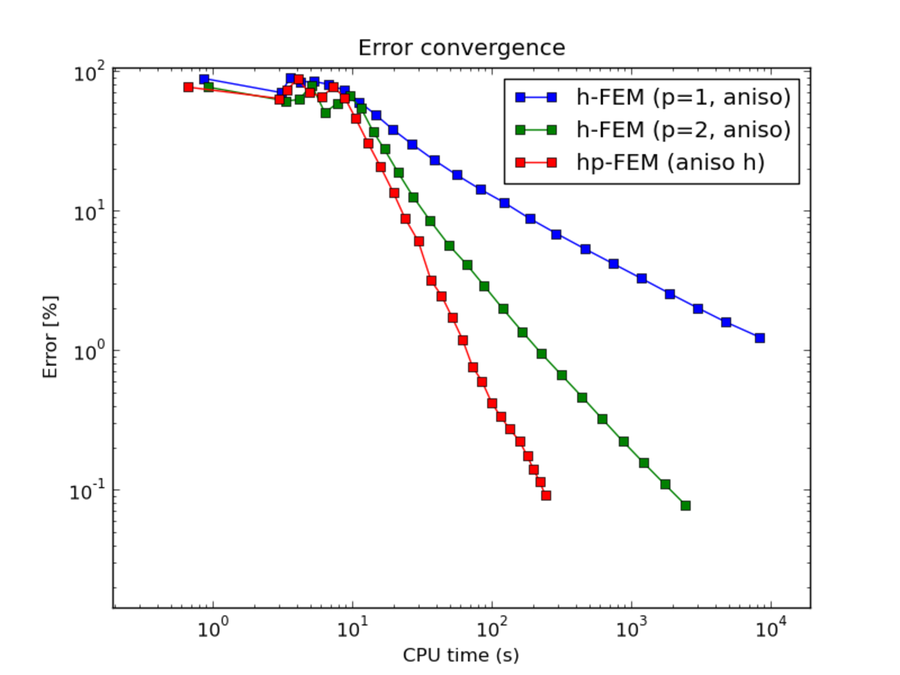
Comparison of h-FEM (p=1), h-FEM (p=2) and hp-FEM with anisotropic refinements¶
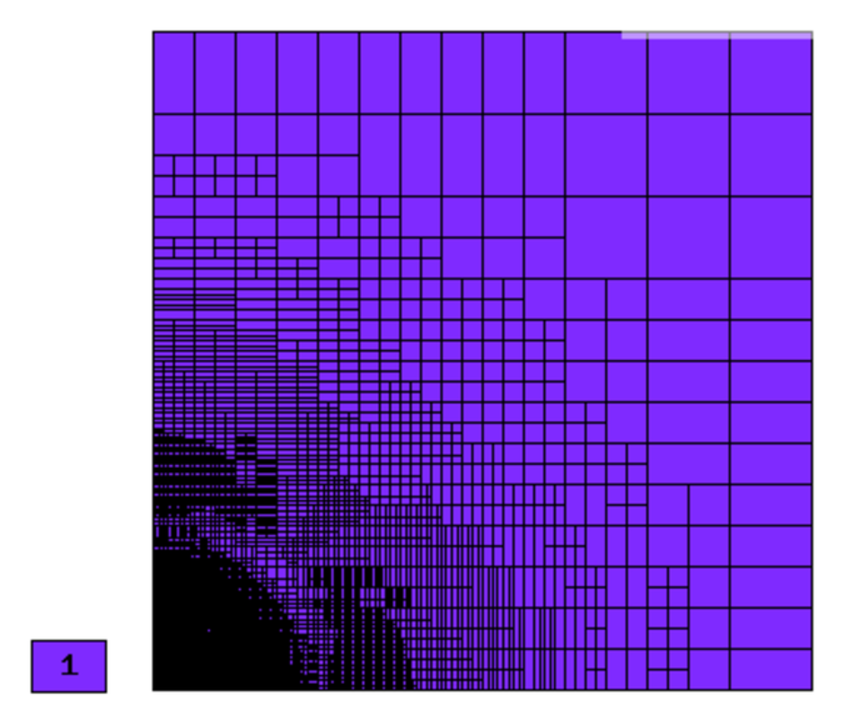
Final mesh (h-FEM, p=1, anisotropic refinements):
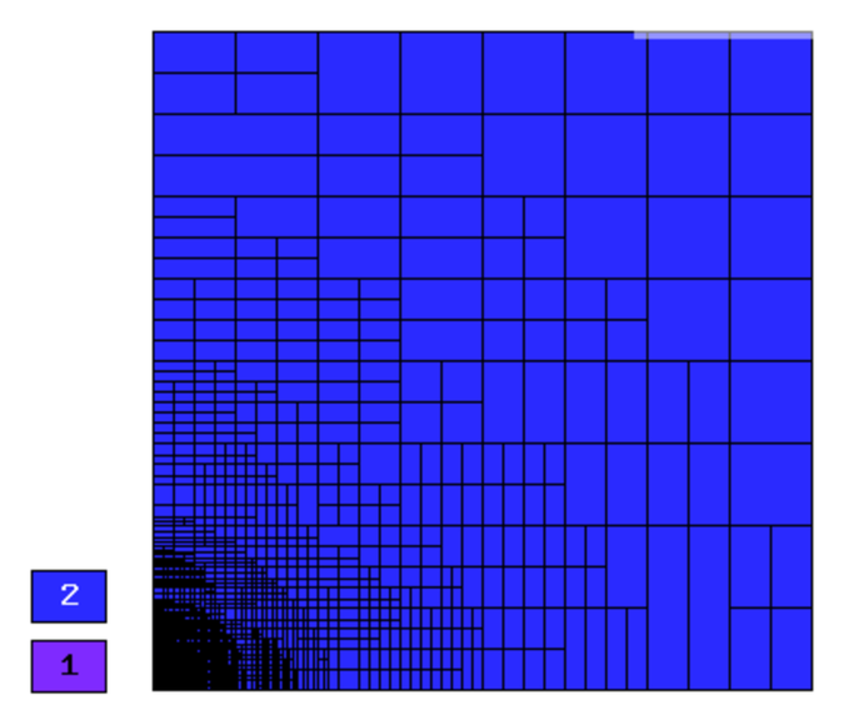
Final mesh (h-FEM, p=2, anisotropic refinements):
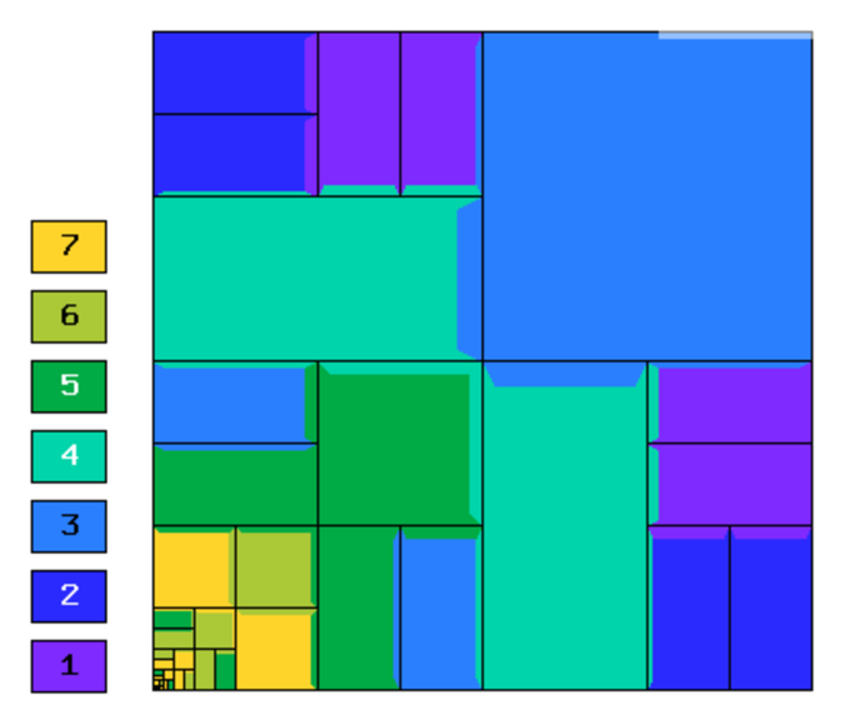
Final mesh (hp-FEM, h-anisotropic refinements):
DOF convergence graphs:
CPU convergence graphs:
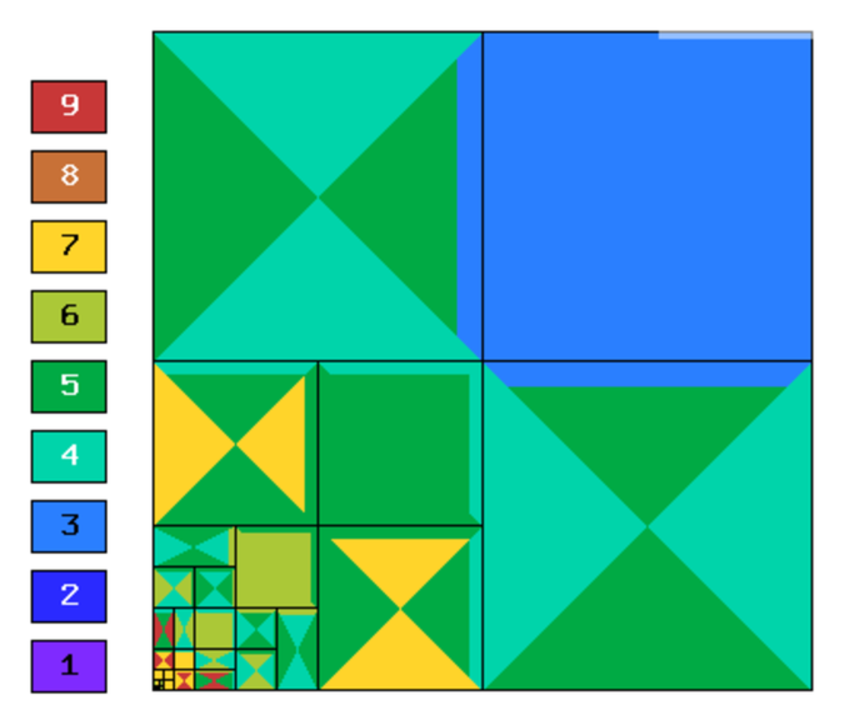
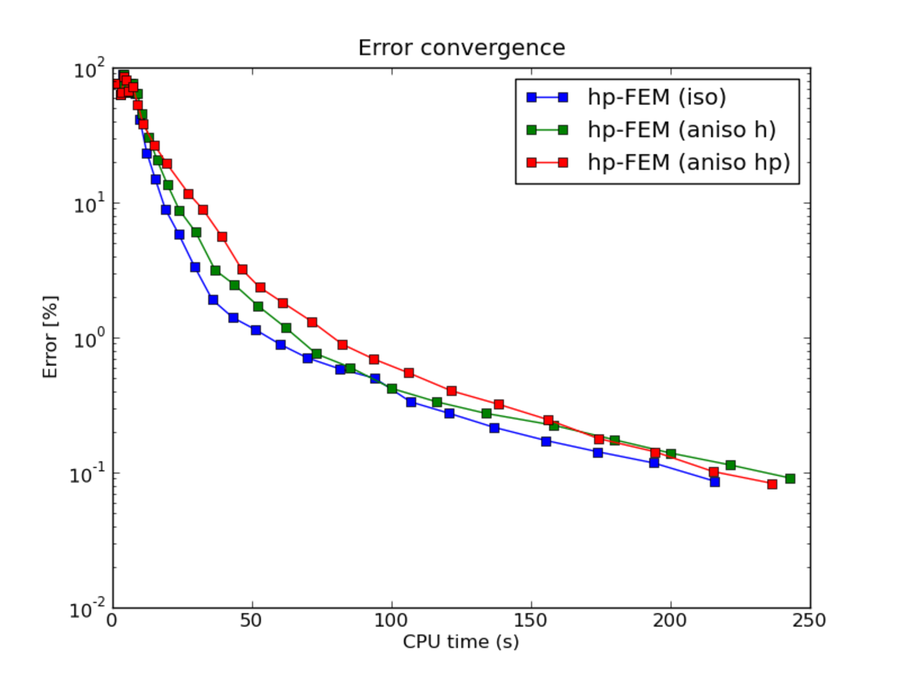
hp-FEM with iso, h-aniso and hp-aniso refinements¶
Final mesh (hp-FEM, isotropic refinements):
Final mesh (hp-FEM, h-anisotropic refinements):
Final mesh (hp-FEM, hp-anisotropic refinements):
DOF convergence graphs:
CPU convergence graphs:
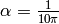 :
: