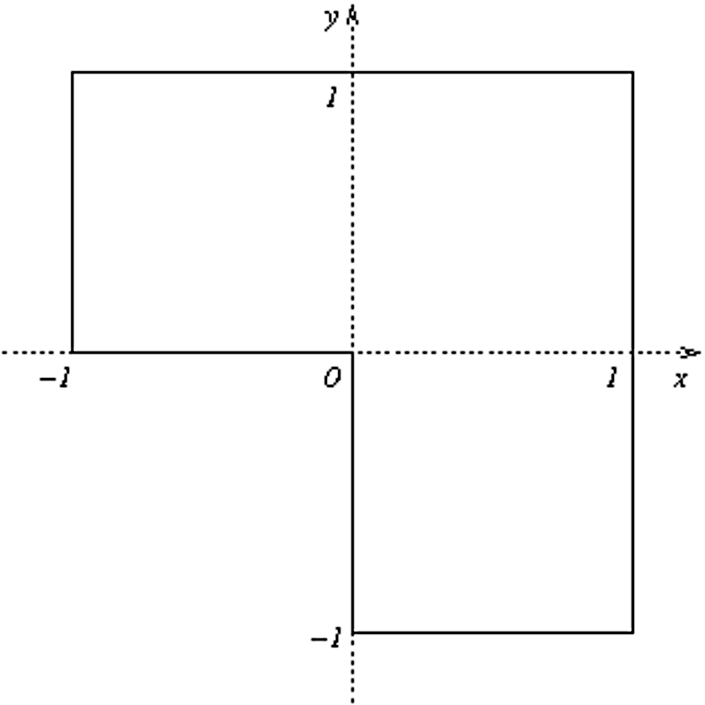
L-Shape (Elliptic)¶
This is a standard adaptivity benchmark whose exact solution is smooth but contains singular gradient in a re-entrant corner.
Boundary conditions¶
Nonconstant Dirichlet, matching the exact solution.
Sample solution¶
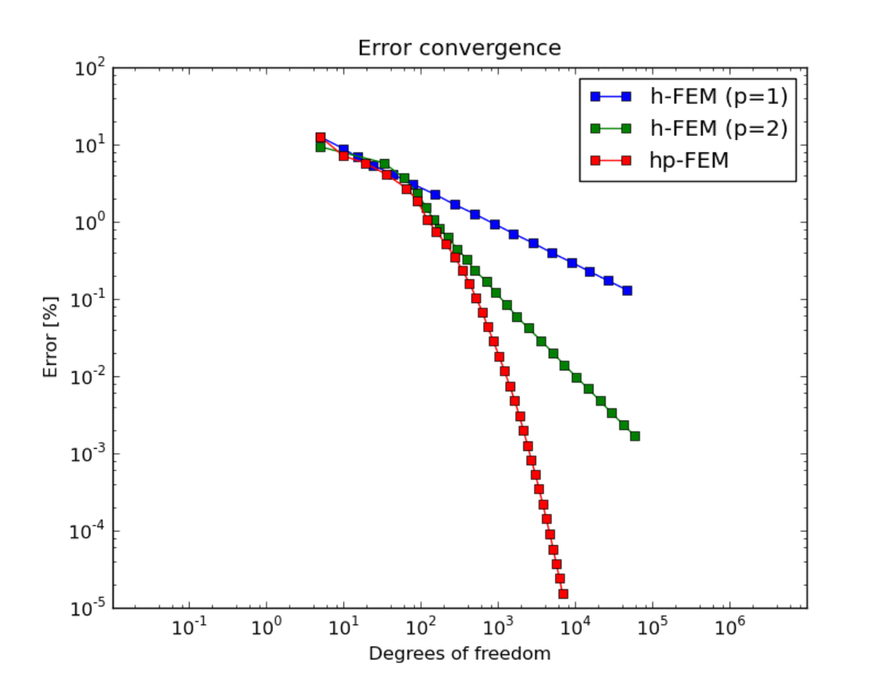
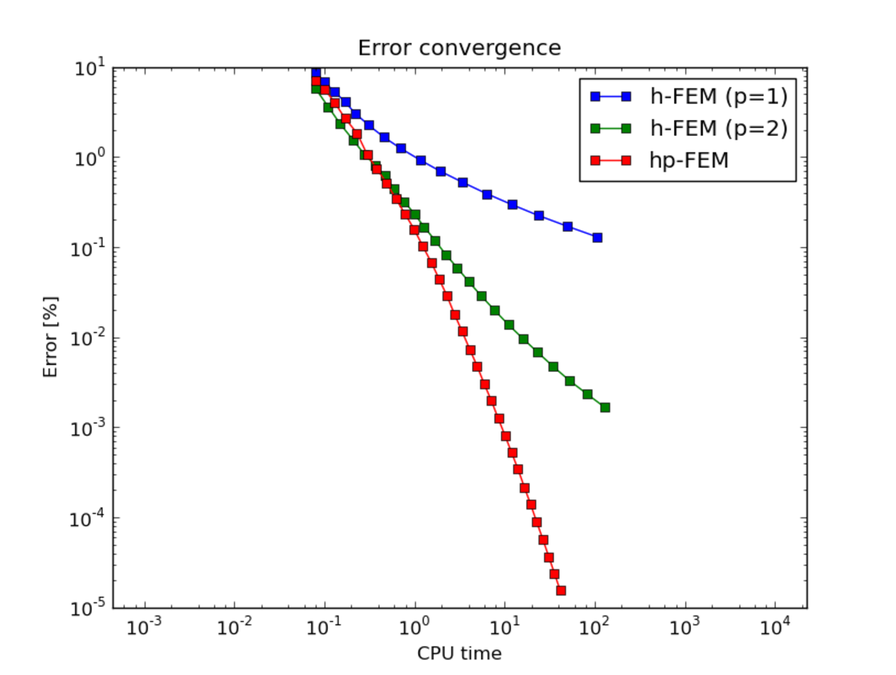
Convergence comparisons¶
Final mesh (h-FEM with linear elements):
Final mesh (h-FEM with quadratic elements):
Final mesh (hp-FEM):
DOF convergence graphs:
CPU time convergence graphs:
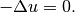
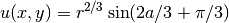
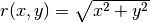 and
and 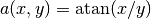 .
.