Interior Layer (Elliptic)¶
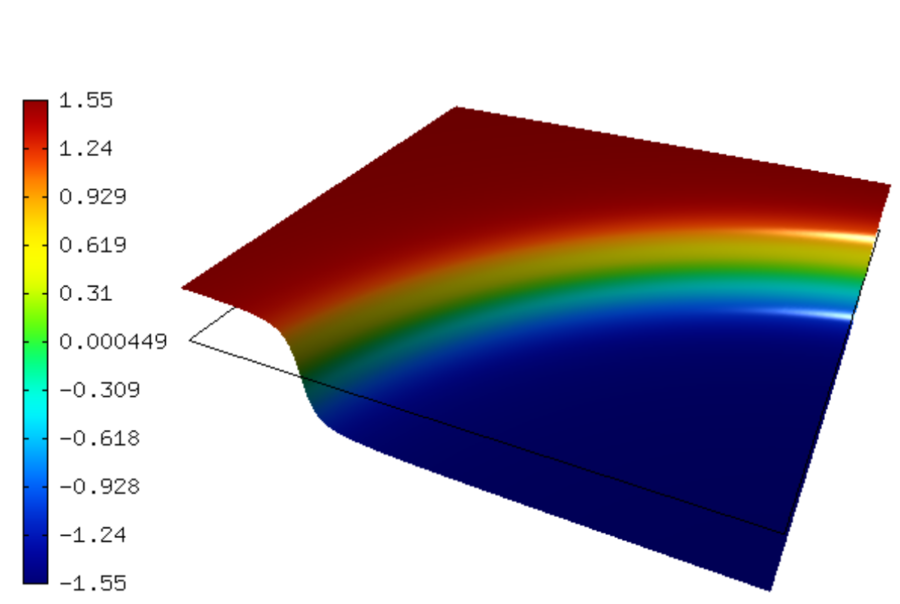
This example has a smooth solution that exhibits a steep interior layer.
Exact solution¶
(2)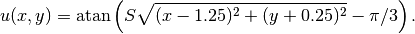
where 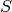 is a parameter (slope of the layer). With larger
is a parameter (slope of the layer). With larger 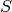 , this problem
becomes difficult for adaptive algorithms, and at the same time the advantage of
adaptive
, this problem
becomes difficult for adaptive algorithms, and at the same time the advantage of
adaptive 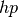 -FEM over adaptive low-order FEM becomes more significant. We will
use
-FEM over adaptive low-order FEM becomes more significant. We will
use 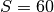 in the following.
in the following.
Boundary conditions¶
Nonconstant Dirichlet, matching the exact solution.
Sample solution¶
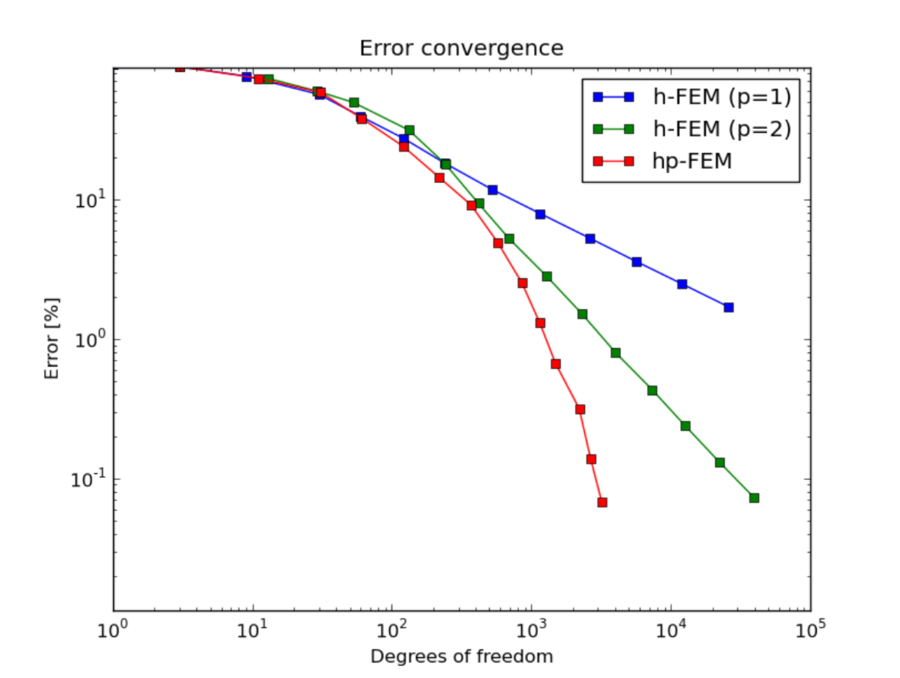
Convergence comparison¶
Final mesh (h-FEM with linear elements):
Final mesh (h-FEM with quadratic elements):
Final mesh (hp-FEM):
DOF convergence graphs:
CPU time convergence graphs:
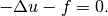
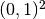 .
.