Jacobian-Free Newton-Krylov Method¶
From the Hermes point of view, the main advantage of Trilinos for nonlinear problems is its implementation of the Jacobian-Free Newton-Krylov Method (JFNK) method. Let us explain how this works:
For a discretized problem of the form
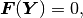
by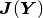 
denote the Jacobian matrix of 
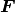. The
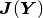JFNK approximates the action of on an arbitrary
vector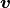 
by
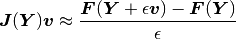
where 
is a small positive real number. Trilinos is smart enough
to figure out the optimal size of by itself.
The only thing one needs to do is to enable evaluation of
the residual vector 
for any given vector 
.
The above approximation is plugged into an iterative matrix solver.
In Trilinos, this functionality is incorporated in the NOX solver.
Preconditioning¶
If the nonlinear problem is ill-conditioned (usually it is) then
preconditioning can be provided to improve the convergence of the
iterative matrix solver. Usually, some simpler part of the Jacobian
matrix 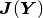is used. For example, in higher-order FEM this
can be the block-diagonal matrix corresponding to vertex-vertex,
edge-edge and bubble-bubble products. For multiphysics problems,
people often use the single-physics diagonal blocks.