Adaptive Multimesh hp-FEM Example (03-system)¶
Model problem¶
We consider a simplified version of the Fitzhugh-Nagumo equation. This equation is a prominent example of activator-inhibitor systems in two-component reaction-diffusion equations, It describes a prototype of an excitable system (e.g., a neuron) and its stationary form is

Here the unknowns 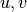 are the voltage and
are the voltage and  -gate, respectively.
The nonlinear function
-gate, respectively.
The nonlinear function

describes how an action potential travels through a nerve. Obviously this system is nonlinear.
Exact solution¶
In order to make it simpler for this tutorial, we replace the function 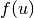 with just
with just  :
:
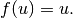
Our computational domain is the square 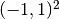 and we consider zero Dirichlet conditions
for both
and we consider zero Dirichlet conditions
for both  and
and  . In order to enable fair convergence comparisons, we will use the following
functions as the exact solution:
. In order to enable fair convergence comparisons, we will use the following
functions as the exact solution:
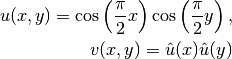
where
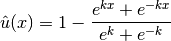
is the exact solution of the one-dimensional singularly perturbed problem

in 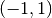 , equipped with zero Dirichlet boundary conditions.
, equipped with zero Dirichlet boundary conditions.
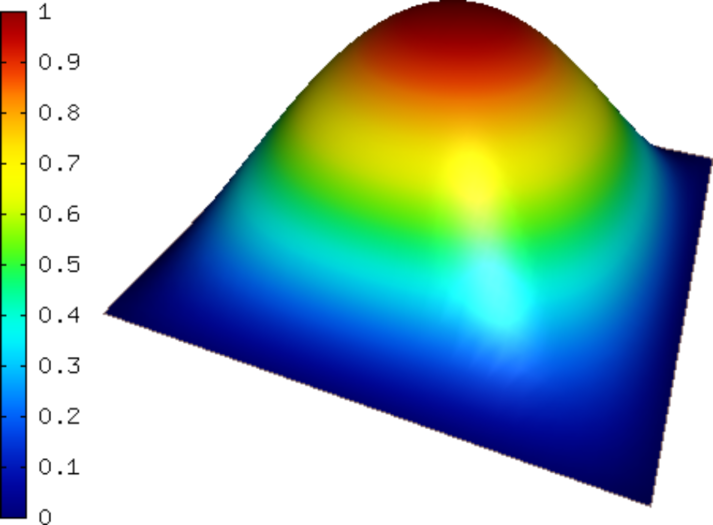
The following two figures show the solutions  and
and  . Notice their
large qualitative differences: While
. Notice their
large qualitative differences: While  is smooth in the entire domain,
is smooth in the entire domain,
 has a thin boundary layer along the boundary:
has a thin boundary layer along the boundary:
Manufactured right-hand side¶
The source functions 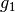 and
and 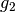 are obtained by inserting
are obtained by inserting 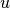 and
and  into the PDE system. These functions are not extremely pretty, but they
are not too bad either - see files definitions.h and definitions.cpp.
into the PDE system. These functions are not extremely pretty, but they
are not too bad either - see files definitions.h and definitions.cpp.
Weak forms¶
The weak forms can be found in the files definitions.h and definitions.cpp. Beware that although each of the forms is actually symmetric, one cannot use the HERMES_SYM flag as in the elasticity equations, since it has a different meaning.
Adaptivity loop¶
The adaptivity workflow is standard. First we construct the reference spaces:
// Construct globally refined reference mesh and setup reference space.
Hermes::vector<Space<double> *>* ref_spaces =
Space<double>::construct_refined_spaces(Hermes::vector<Space<double> *>(&u_space, &v_space));
Next we pass the new reference Spaces to the Newton solver:
newton.set_spaces(ref_spaces);
And we solve the problem using the Newton’s method:
// Perform Newton's iteration.
try
{
newton.solve(coeff_vec);
}
catch(Hermes::Exceptions::Exception e)
{
e.printMsg();
}
Next we translate the coefficient vector into the two Solutions, project reference solutions to the coarse meshes, calculate error estimates, calculate exact errors (optional), and adapt the coarse meshes. For details on the last steps see the filemain.cpp.
Sample results¶
Now we can show some numerical results.
First let us show the resulting meshes for 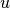 and
and  obtained using
conventional (single-mesh) hp-FEM: 9,330 DOF (4665 for each solution component).
obtained using
conventional (single-mesh) hp-FEM: 9,330 DOF (4665 for each solution component).
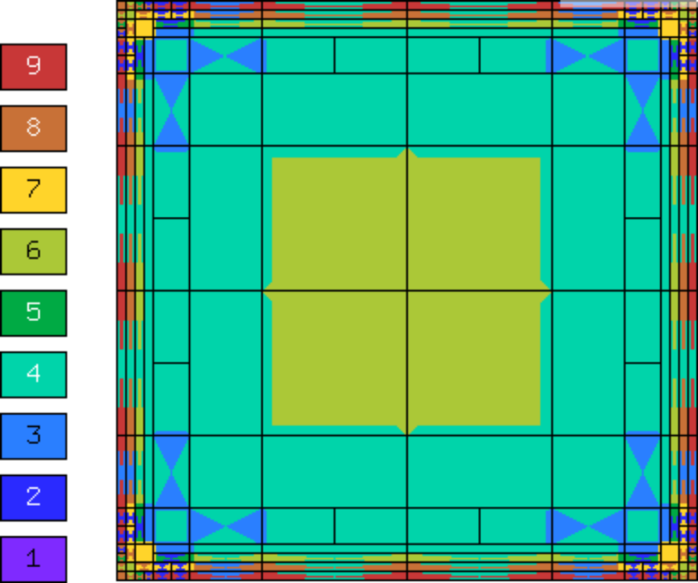
Next we show the resulting meshes for 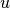 and
and  obtained using
the multimesh hp-FEM: 1,723 DOF (49 DOF for
obtained using
the multimesh hp-FEM: 1,723 DOF (49 DOF for 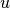 and
and 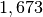 for
for  ).
).
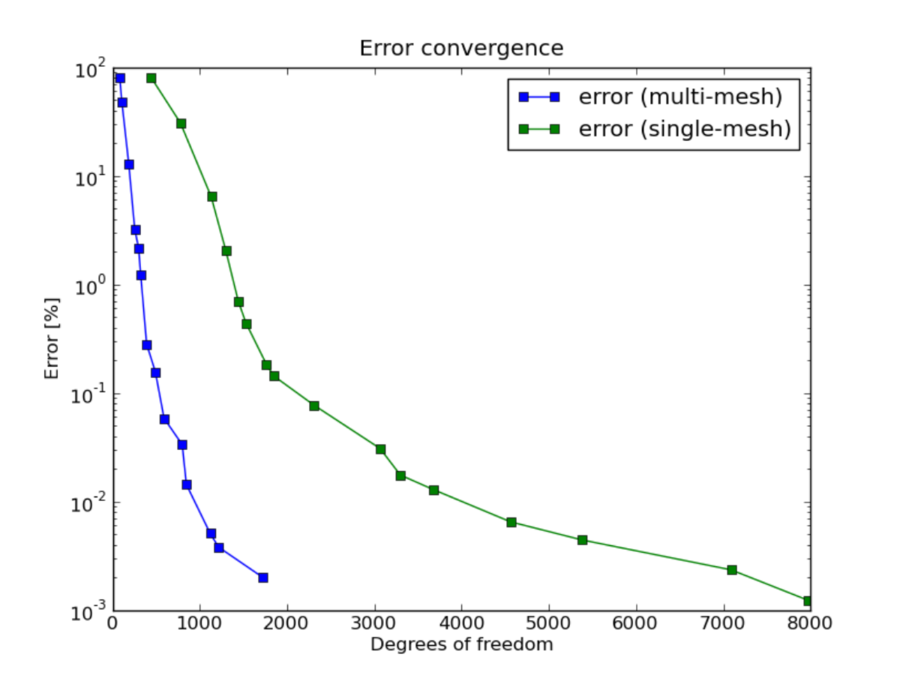
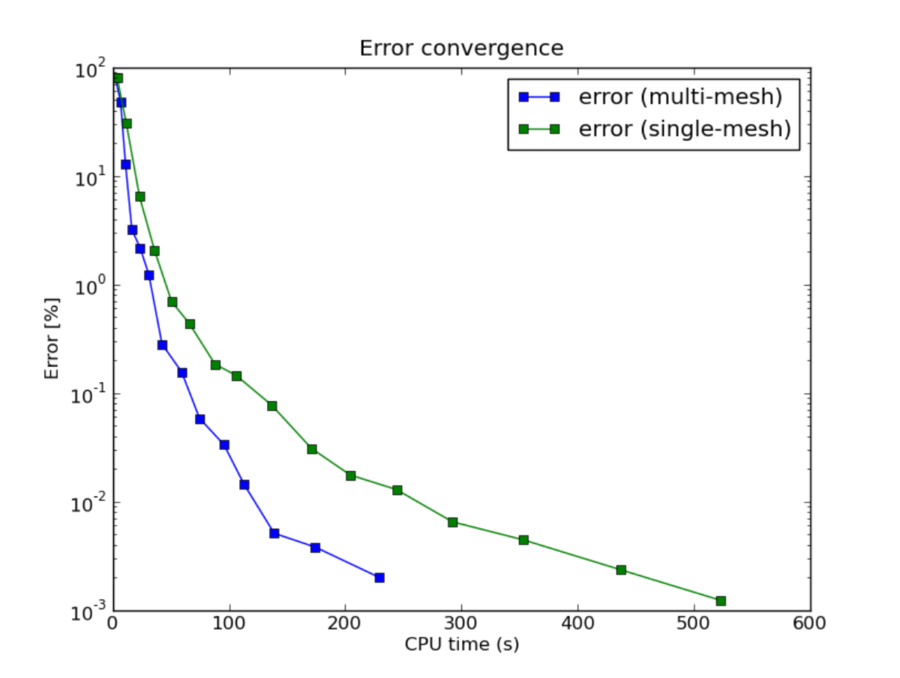
Finally let us compare the DOF and CPU convergence graphs for both cases:
DOF convergence graphs:
CPU time convergence graphs: