Newton’s Method with Spline Nonlinearity (02-newton-spline)

Model problem

We will use the same model problem as in examples 01-picard and 02-newton-analytic. The only difference will be a spline nonlinearity .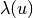

Defining a cubic spline

The CubicSpline class is a descendant of HermesFunction. It is initialized with a sequence of points and function values at these points. As solution values are passed into the spline, one has to be careful to define it on a sufficiently wide range of values. In this concrete example, we use the points:

Hermes::vector<double> lambda_pts(-2.0, -1.5, -1.0, -0.5, 0.0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 4.0, 5.0);

For simplicity, we use a macro

#define lambda_macro(x) (1 + pow(x, 4))

to fill a Hermes::vector of the values,

Hermes::vector<double> lambda_val;
for (unsigned int i = 0; i < lambda_pts.size(); i++) lambda_val.push_back(lambda_macro(lambda_pts[i]));

but in practice of course the values can be arbitrary. To finish the spline, one needs to provide two extra conditions, which can be either the first or the second derivatives at the endpoints. For this example we choose zero second derivatives, forming a natural cubic spline:

double bc_left = 0.0;
double bc_right = 0.0;
bool first_der_left = false;
bool first_der_right = false;

The user also has to tell what Hermes should do when the spline is evaluated outside its area of definition. Two options are provided - either the spline is extended as a constant, using the last value at the endpoint, or it is extended as a linear function using the derivative at the endpoint. In this example, we choose to extrapolate the derivative if this happens:

bool extrapolate_der_left = true;
bool extrapolate_der_right = true;

Then the constructor of the CubicSpline class is called:

CubicSpline lambda(lambda_pts, lambda_val, bc_left, bc_right, first_der_left, first_der_right,
                   extrapolate_der_left, extrapolate_der_right);

Plotting the spline for visual control

The spline can be plot using:

info("Saving cubic spline into a Pylab file spline.dat.");
double interval_extension = 3.0; // The interval of definition of the spline will be
                                 // extended by "interval_extension" on both sides.
lambda.plot("spline.dat", interval_extension);

and visualized, for example, via Gnuplot or Matplotlib.

Initializing the weak formulation

Since the CubicSpline class is just another descendant of HermesFunction, we can use the DefaultWeakFormPoisson class as in example 02-newton-analytic:

// Initialize the weak formulation.
Hermes2DFunction<double> src(-heat_src);
DefaultWeakFormPoisson<double> wf(HERMES_ANY, &lambda, &src);

Convergence

The convergence is similar in terms of thenumber of iterations to example 02-newton-analytic, but it is faster in terms of the CPU time:

I Saving cubic spline into a Pylab file spline.dat.
I ndof: 961
I Projecting to obtain initial vector for the Newton's method.
I ---- Newton initial residual norm: 1172.56
I ---- Newton iter 1, residual norm: 957.004
I ---- Newton iter 2, residual norm: 296.191
I ---- Newton iter 3, residual norm: 78.7839
I ---- Newton iter 4, residual norm: 13.2494
I ---- Newton iter 5, residual norm: 0.601854
I ---- Newton iter 6, residual norm: 0.00134473
I ---- Newton iter 7, residual norm: 1.54663e-08
  << close all views to continue >>

Sample results

The resulting approximation is visually the same as in examples 01-picard and 02-newton-analytic.