Nonconstant Dirichlet BC (04-bc-dirichlet)¶
Let us keep the equation from the previous example P01/03-poisson,
(1)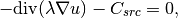
but the boundary conditions will be modified to
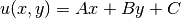
where 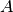 ,
, 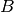 and
and 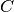 are real constants.
are real constants.
Subclassing EssentialBoundaryCondition¶
This is done by defining a descendant of the EssentialBoundaryCondition class:
class CustomDirichletCondition : public EssentialBoundaryCondition<double>
{
public:
CustomDirichletCondition(Hermes::vector<std::string> markers, double A, double B, double C);
virtual EssentialBoundaryCondition<double>::EssentialBCValueType get_value_type() const;
virtual double value(double x, double y, double n_x, double n_y, double t_x, double t_y) const;
protected:
double A, B, C;
};
The methods are defined in the file definitions.cpp as follows:
CustomDirichletCondition::CustomDirichletCondition(Hermes::vector<std::string> markers,
double A, double B, double C)
: EssentialBoundaryCondition<double>(markers), A(A), B(B), C(C)
{
}
EssentialBoundaryCondition<double>::EssentialBCValueType CustomDirichletCondition::get_value_type() const
{
return EssentialBoundaryCondition<double>::BC_FUNCTION;
}
double CustomDirichletCondition::value(double x, double y, double n_x, double n_y,
double t_x, double t_y) const
{
return A*x + B*y + C;
}
The custom boundary condition class is used as follows:
// Initialize boundary conditions.
CustomDirichletCondition bc_essential(Hermes::vector<std::string>("Bottom", "Inner", "Outer", "Left"),
BDY_A_PARAM, BDY_B_PARAM, BDY_C_PARAM);
EssentialBCs<double> bcs(&bc_essential);
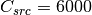 ,
, 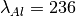 ,
, 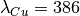 ,
,
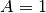 ,
, 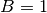 and
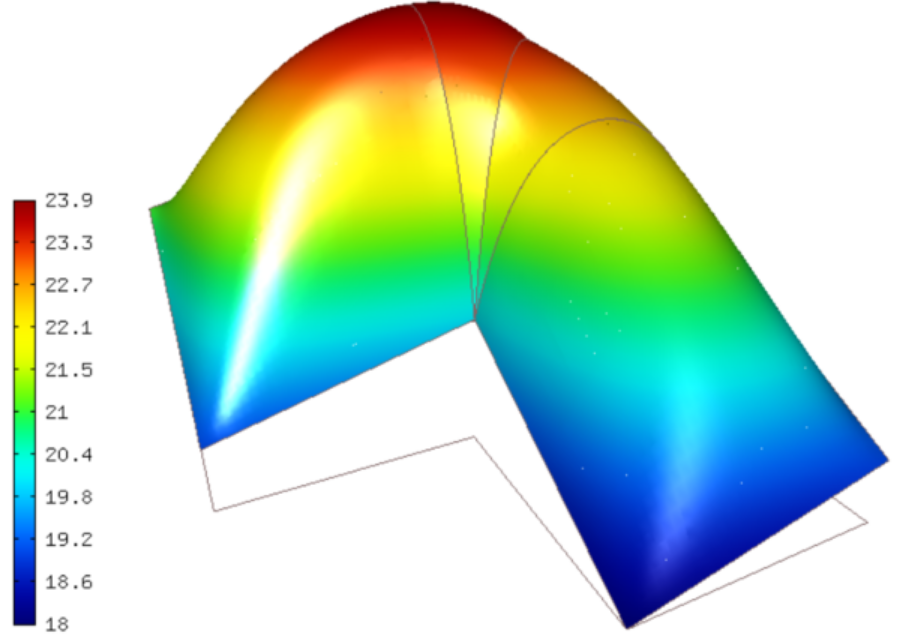
and 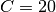 is shown below:
is shown below: