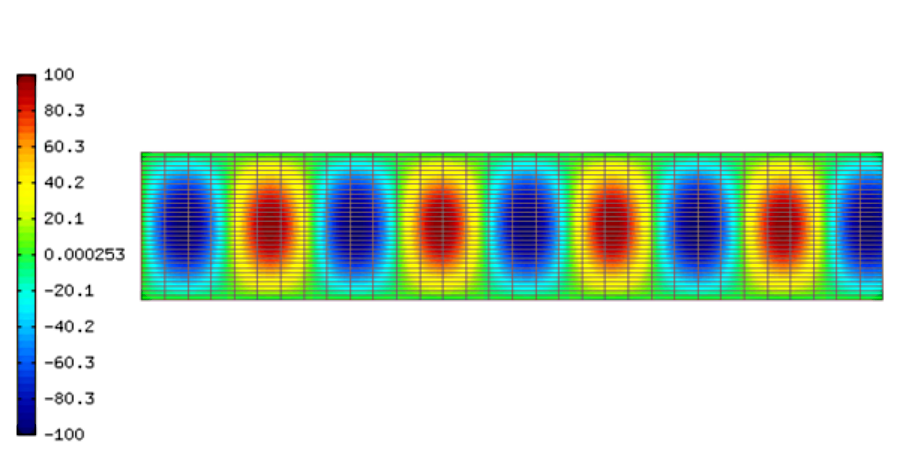
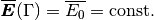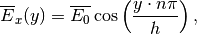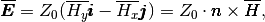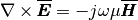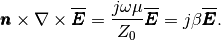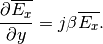Waveguide¶

By David Panek, University of West Bohemia, Czech Republic.

Mathematical description of waveguides¶

Mathematical description of waveguides is given by the Maxwell’s equations

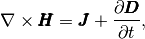
(1) $\nabla \times {\pmb{H}} &= {\pmb{J}} + \frac{\partial {\pmb{D}}}{\partial t},$

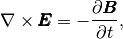
(2) $\nabla \times {\pmb{E}} &= - \frac{\partial {\pmb{B}}}{\partial t},$

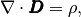
(3) $\nabla \cdot {\pmb{D}} &= \rho,$

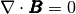
(4) $\nabla \cdot {\pmb{B}} &= 0$

where

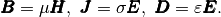
(5) ${\pmb{B}} = \mu {\pmb{H}}, \ {\pmb{J}} = \sigma {\pmb{E}}, \ {\pmb{D}} = \varepsilon {\pmb{E}}.$

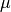Here $\varepsilon$ means permittivity, $\mu$ permeability and 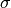$\sigma$ stands for electric conductivity. For waveguides analysis, material properties are often considered constant and isotropic. After substituting material properties (5) into equations (1) and (2), we get

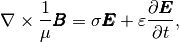
(6) $\nabla \times \frac{1}{\mu} {\pmb{B}} &= \sigma {\pmb{E}} + \varepsilon \frac{\partial {\pmb{E}}}{\partial t},$

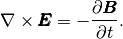
(7) $\nabla \times {\pmb{E}} &= - \frac{\partial {\pmb{B}}}{\partial t}.$

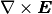If the vector operator $\mathrm{curl}$ is applied on the equation (7), it is possible to substitute $\nabla \times \pmb{E}$ from the equation (6) and get the wave equation for the electric field in the form

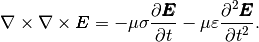
(8) $\nabla \times \nabla \times \pmb{E} = - \mu \sigma \frac{\partial {\pmb{E}}}{\partial t} - \mu \varepsilon \frac{\partial^2 {\pmb{E}}}{\partial t^2}.$

In a medium with zero charge density 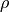$\rho$ it is useful to apply the vector identity

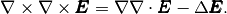
(9) $\nabla \times \nabla \times \pmb{E} = \nabla \nabla \cdot \pmb{E} - \Delta \pmb{E}.$

Since 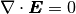$\nabla \cdot \pmb{E} = 0$ ), the wave equation (8) can be simplified to

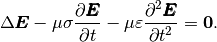
(10) $\Delta \pmb{E} - \mu \sigma \frac{\partial {\pmb{E}}}{\partial t} - \mu \varepsilon \frac{\partial^2 {\pmb{E}}}{\partial t^2} = \mathbf{0}.$

For many technical problems it is sufficient to know the solution in the frequency domain. After applying the Fourier transform, equation (10) becomes

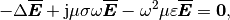
(11) $-\Delta \overline{\pmb{E}} + \mathrm{j} \mu \sigma \omega \overline{\pmb{E}} - \omega^2 \mu \varepsilon \overline{{\pmb{E}}} = \mathbf{0},$

which is the Helmholtz equation.

Decomposition into two real equations¶

The electric field 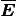$\overline{\pmb{E}}$ can be written as

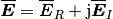
(12) $\overline{\pmb{E}} = \overline{\pmb{E}}_R + \mathrm{j} \overline{\pmb{E}}_I$

Substituting into the original equation, we obtain

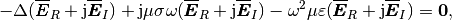
(13) $-\Delta (\overline{\pmb{E}}_R + \mathrm{j} \overline{\pmb{E}}_I) + \mathrm{j} \mu \sigma \omega (\overline{\pmb{E}}_R + \mathrm{j} \overline{\pmb{E}}_I) - \omega^2 \mu \varepsilon (\overline{\pmb{E}}_R + \mathrm{j} \overline{\pmb{E}}_I) = \mathbf{0},$

Last, comparing the real and imaginary numbers in the equation, we have

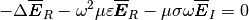
(14) $-\Delta \overline{\pmb{E}}_R - \omega^2 \mu \varepsilon \overline{\pmb{E}}_R - \mu \sigma \omega \overline{\pmb{E}}_I = 0$

and

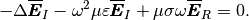
(15) $-\Delta \overline{\pmb{E}}_I - \omega^2 \mu \varepsilon \overline{\pmb{E}}_I + \mu \sigma \omega \overline{\pmb{E}}_R = 0.$

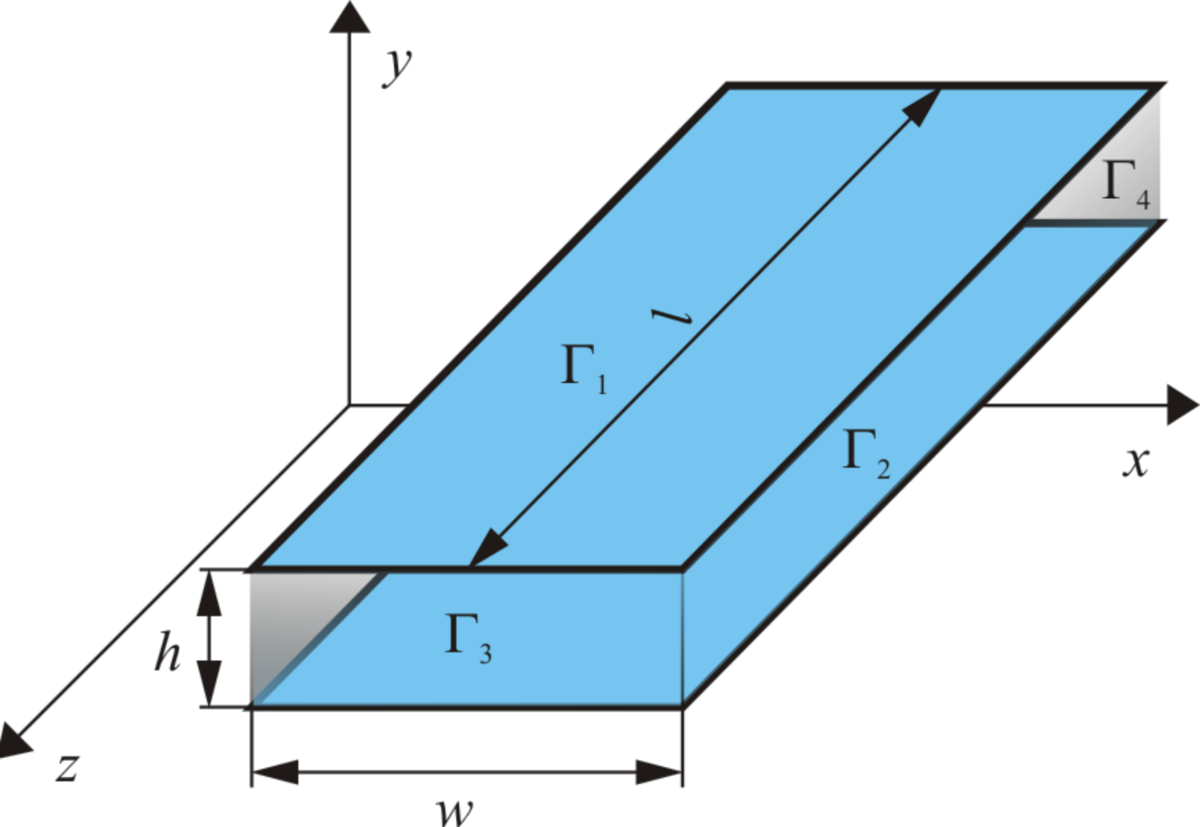
Parallel plate waveguide¶

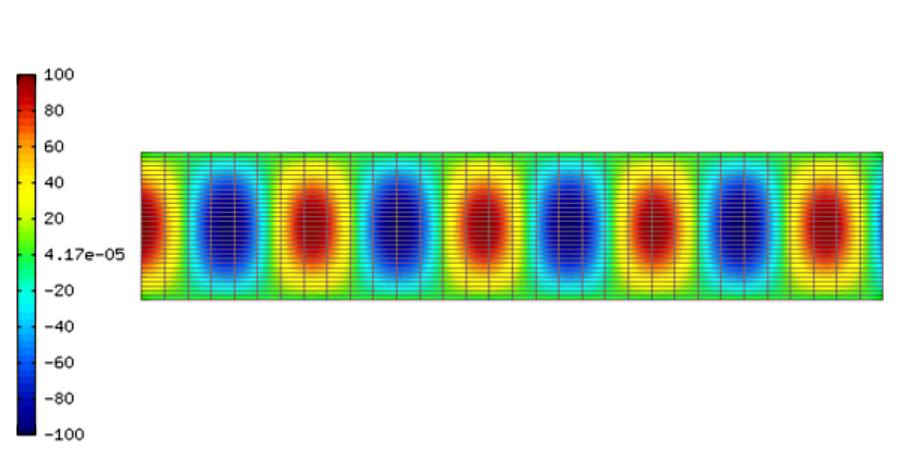
Parallel plate waveguide is the simplest type of guide that supports TM (transversal magnetic) and TE (transversal electric) modes. This kind of guide allows also TEM (transversal electric and magnetic) mode.

Mathematical model - TE modes¶

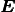Suppose that the electromagnetic wave is propagating in the direction $z$ , then the component of the vector $\pmb{E}$ in the direction of the propagation is equal to zero

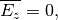
(16) $\overline{E_z} = 0,$

thus it is possible to solve the electric field in the parallel plate waveguide as a two-dimensional Helmholtz problem

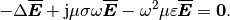
(17) $-\Delta \overline{\pmb{E}} + \mathrm{j} \mu \sigma \omega \overline{\pmb{E}} - \omega^2 \mu \varepsilon \overline{{\pmb{E}}} = \mathbf{0}.$

The conducting plates (boundary 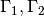$\Gamma_1, \Gamma_2$ ) are usually supposed to be perfectly conductive, which can be modeled using the perfect conductor boundary condition

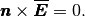
(18) $\pmb{n} \times \overline{\pmb{E}} = 0.$

For the geometry in the above figure the expression (18) is reduced to a zero Dirichlet boundary condition

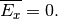
(19) $\overline{E_x} = 0.$

For the boundaries 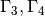$\Gamma_3, \Gamma_4$ , the following types of boundary conditions can be used:

Electric field (Dirichlet boundary condition)¶

(20) $\overline{\pmb{E}}(\Gamma) = \overline{E_0} = \mathrm{const}.$

Note that for TE modes (and for the geometry shown above), a natural boundary condition is described by the expression

(21) $\overline{E}_x(y) = \overline{E_0} \cos\left(\frac{y \cdot n \pi}{h} \right),$

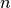where $n$ stands for a mode.

Impedance matching (Newton boundary condition)¶

For harmonic TE mode waves the following relation holds:

(22) $\overline{\pmb{E}} = Z_0 (\overline{H_y} \pmb{i} - \overline{H_x} \pmb{j}) = Z_0 \cdot \pmb{n} \times \overline{\pmb{H}},$

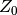where $Z_0$ is the wave impedance. At the same time the second Maxwell equation

(23) $\nabla\times \overline{{\pmb{E}}} = -j \omega \mu \overline{\pmb{H}}$

must be satisfied. From quations (22) and (23) it is possible to derive impedance matching boundary condition in the form

(24) $\pmb{n} \times \nabla \times \overline{\pmb{E}} = \frac{j \omega \mu }{Z_0} \overline{\pmb{E}} = j \beta \overline{\pmb{E}}.$

For a given geometry the equation (24) can be reduced to the Newton boundary condition in the form

(25) $\frac{\partial \overline{E_x}}{\partial y} = j \beta \overline{E_x}.$

Material parameters¶

const double epsr = 1.0;                    // Relative permittivity
const double eps0 = 8.85418782e-12;         // Permittivity of vacuum F/m
const double mur = 1.0;                     // Relative permeablity
const double mu0 = 4*M_PI*1e-7;             // Permeability of vacuum H/m
const double frequency = 3e9;               // Frequency MHz
const double omega = 2*M_PI * frequency;    // Angular velocity
const double sigma = 0;                     // Conductivity Ohm/m

Boundary conditions¶

There are three possible types of boundary conditions:

Zero Dirichlet boundary conditions.

Nonzero Dirichlet boundary conditions.

Newton boundary conditions.

Waveguide¶

Mathematical description of waveguides¶

Decomposition into two real equations¶

Parallel plate waveguide¶

Mathematical model - TE modes¶

Electric field (Dirichlet boundary condition)¶

Impedance matching (Newton boundary condition)¶

Material parameters¶

Boundary conditions¶

Sample results¶

Table Of Contents

Previous topic

Next topic

Navigation

Waveguide¶

Mathematical description of waveguides¶

Decomposition into two real equations¶

Parallel plate waveguide¶

Mathematical model - TE modes¶

Electric field (Dirichlet boundary condition)¶

Impedance matching (Newton boundary condition)¶

Material parameters¶

Boundary conditions¶

Sample results¶

Table Of Contents

Previous topic

Next topic

Quick search

Navigation