NURBS Mesh (01-nurbs-mesh)

This example shows how to use full-featured NURBS to define curved boundary edges. Recall that simplified format is available for circular arcs, as was shown in example 03-poisson.

General description of NURBS

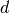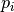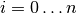Every NURBS curve is defined by its degree, control points with weights and the knot vector. The degree is a positive integer, usually 1, 2, 3 or 5. Lines and polylines are of degree 1, circles have degree 2 and free-form curves are of degree 3 or 5. The control points , , are the main tool for changing the shape of the curve. A curve of degree 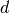must have at least control points. In Hermes, the endpoints of the edge are always assumed to be the first and last control points and therefore only the inner control points are listed in the mesh file. There is a weight 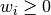for every control point, that influences the shape of the curve in its vicinity. If 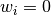then 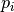has no effect on the shape. As 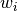increases, the curve is pulled towards .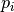

The knot vector is a sequence of 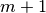values that determines how much and where the control points influence the shape. The relation 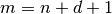must hold. The sequence is nondecreasing, , and divides the whole interval into smaller intervals which determine the area of influence of the control points. Since the curve has to start and end at the edge vertices, the knot vector in Hermes always starts with zeros and ends with ones. Only the inner knots are listed in the above definition of the variable curves, where 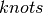is a simple list of real values.

Sample mesh file

The comments in the mesh file “domain-4.mesh” are self-explanatory:

a = 1.0
ma = -1.0

#b = sqrt(2)/2
b = 0.70710678118654757

ab = 0.70710678118654757

a1 = 0.25
a2 = 0.5
a3 = 0.75

c1 = -1.5
c2 = -0.5

b1 = -1.5
b2 = -2

d1 = 0.2
d2 = 0.7

vertices = [
  [ 0,  ma],    # vertex 0
  [ a, ma ],    # vertex 1
  [ ma, 0 ],    # vertex 2
  [ 0, 0 ],     # vertex 3
  [ a, 0 ],     # vertex 4
  [ ma, a ],    # vertex 5
  [ 0, a ],     # vertex 6
  [ ab, ab ]  # vertex 7
]

elements = [
  [ 0, 1, 4, 3, "1"  ],   # quad 0
  [ 3, 4, 7,    "1"  ],   # tri 1
  [ 3, 7, 6,    "2" ],  # tri 2
  [ 2, 3, 6, 5, "2" ]   # quad 3
]

boundaries = [
  [ 0, 1, "Bottom Layer" ],
  [ 1, 4, "Outer Layer" ],
  [ 3, 0, "Inner Layer" ],
  [ 4, 7, "Outer Layer" ],
  [ 7, 6, "Outer Layer" ],
  [ 2, 3, "Inner Layer" ],
  [ 6, 5, "Outer Layer" ],
  [ 5, 2, "Left Boundary" ]
]

degree_1 = 4

inner_points_1 = [
  [ a1, c1, 1.0 ],
  [ a2, c2, 1.0 ],
  [ a3, c1, 1.0 ]
]

knots 1 = [
  0, 0, 0, 1, 1, 1
]

degree_2 = 3

inner_points_2 = [
  [ b1, d1, 0.5],
  [ b2, d2, 1.0]
]

knots_2 = [
  0, 0, 0, 1, 1, 1
]

angle_1 = 45

curves = [
  [ 4, 7, angle_1 ],  # circular arc with central angle of 45 degrees
  [ 7, 6, 45 ],       # circular arc with central angle of 45 degrees
  [ 0, 1, degree_1, inner_points_1, knots 1],
  [ 2, 5, degree_2, inner_points_2, knots_2]
]

Resulting mesh image