Finite Element Space (02-space)

Hermes follows the mathematical concept of FEM closely – after reading a mesh, the user has to create a finite element space on it.

Spaces available in Hermes

The following predefined spaces are currently available:

• H1Space - the most common FE space of continuous, piecewise-polynomial functions:

• HcurlSpace - FE space of vector-valued functions discontinuous along mesh edges, with continuous tangential component on the edges:

• HdivSpace - FE space of vector-valued functions discontinuous along mesh edges, with continuous normal component on the edges:

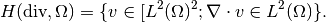
• L2Space - FE space of functions discontinuous along mesh edges:

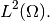
All these spaces admit higher-order elements, arbitrary-level hanging nodes, automatic hp-adaptivity, and they can be combined arbitrarily in multi-physics problems via the multimesh hp-FEM.

Structure of higher-order basis functions in H1Space

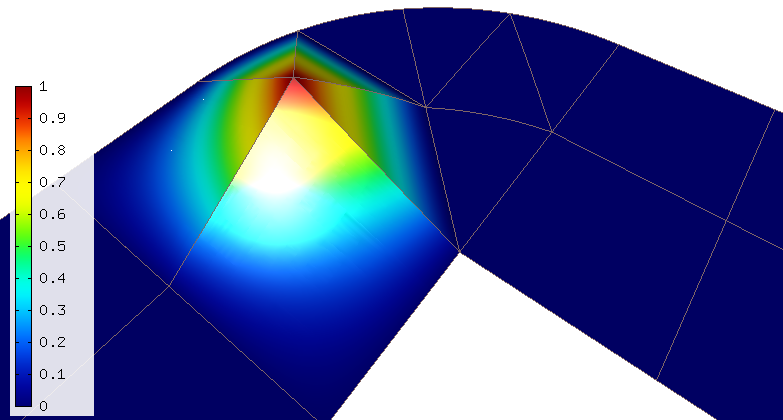
In 2D, there are three types of basis functions. First, of course, the standard piecewise linear or bilinear vertex functions (“pyramids”) that are used in the lowest-order FEM:

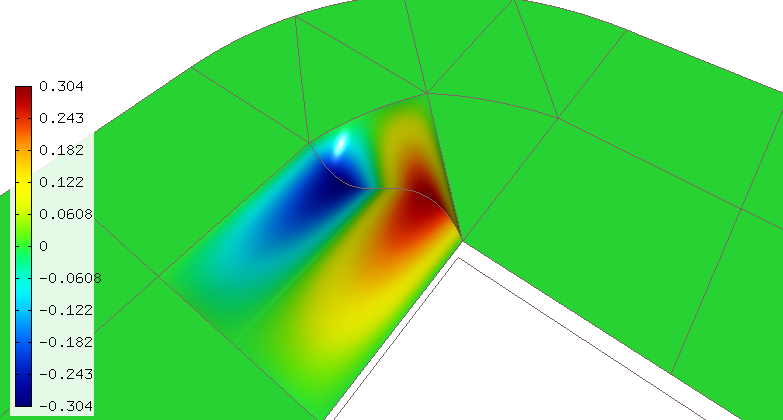
Next there are edge functions which are associated with mesh edges. They are nonzero only in the one or two elements that are adjacent to that edge. The following figure shows an example of a cubic edge function:

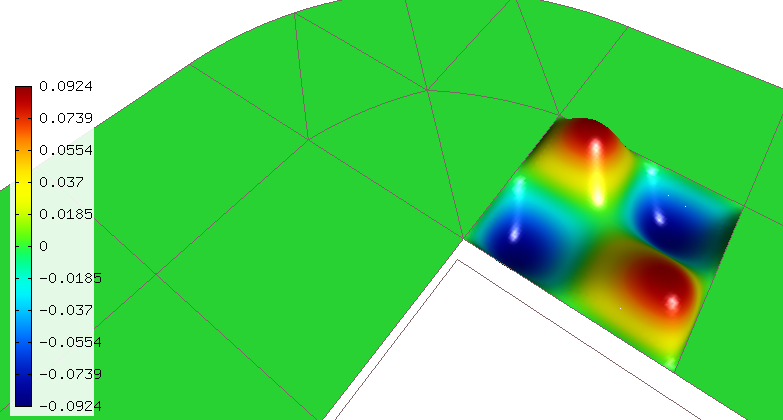
Last there are bubble functions that are local to element interiors. The following figure shows an example of a bicubic bubble function in a quadrilateral element:

Higher-order basis functions can be defined in many different ways. A particular set of polynomials is called shapeset. Using a good shapeset is crucial for the performance of the hp-FEM. No shapeset can be optimal for all possible operators. Therefore, Hermes offers several shapesets from which you need to choose one when creating a FE space. The ones which perform best in most computations, according to our experience, are simply called H1Shapeset, HcurlShapeset, HdivShapeset and L2Shapeset. Other shapesets can be found in the directory “src/shapeset”.

Creating an H1Space

An instance of a real-valued H1Space can be created as follows:

// Create a real-valued H1 space with default shapeset and natural BC.
H1Space<double> space(&mesh, P_INIT);

The two arguments used here are:

• Pointer to a mesh.
• Uniform initial polynomial degree of all mesh elements.

An instance of a complex-valued H1Space can be created analogously:

// Create a complex-valued H1 space with default shapeset and natural BC.
H1Space<complex> space(&mesh, P_INIT);

In the next example 03-poisson we will see that in addition to these two parameters, one can also use a pointer to the EssentialBCs class (if essential boundary conditions are used).

Setting element orders individually

Polynomial degrees of elements can be set individually by calling the methods

virtual void set_element_order(int id, int order);

or

virtual void set_element_orders(int* elem_orders);

of the class Space. There are additional methods in this class that can be used to manipulate element orders, see the Doxygen docs for the Space class.

It is worth mentioning that element degrees are stored in Space, not in Mesh. The reason is that in Hermes one can have several finite element spaces with individual element degrees on one mesh. The Mesh class only stores geometrical information such as coordinates and connectivities

Visualizing basis functions

Hermes can visualize the basis of each Space. Similarly to MeshView, one can create a BaseView object and use it to display the entire basis. The BaseView class was also used to generate the images above:

// View FE basis functions.
BaseView<double> bview("Finite Element Space", new WinGeom(0, 0, 440, 350));
bview.fix_scale_width(50);
bview.show(&space, HERMES_EPS_HIGH);

Press ‘3’ for 3D view. VectorBaseView has to be used for vector-valued approximations in spaces Hcurl and Hdiv. One can cycle through all basis functions in the window using the arrow keys. Pressing the left arrow at the beginning will show the Dirichlet lift (a function that represents Dirichlet boundary conditions).