Gross-Pitaevski Equation¶
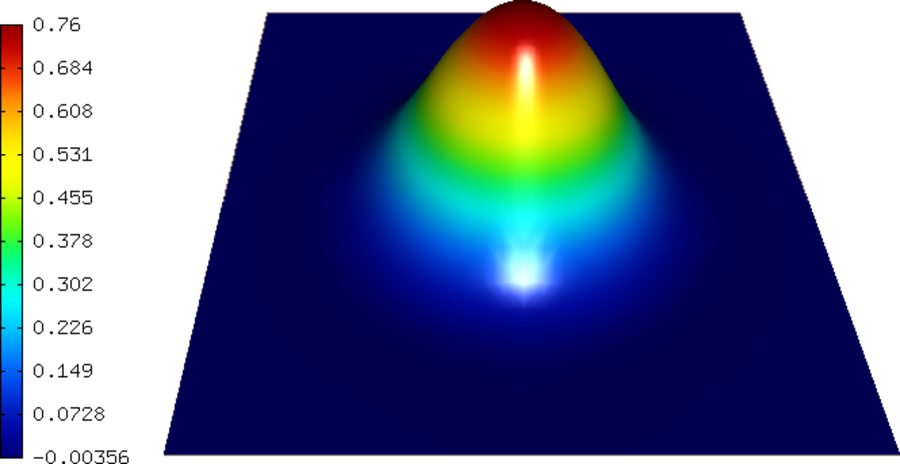
In this example we use the Newton’s method to solve the nonlinear complex-valued time-dependent Gross-Pitaevski equation. This equation describes the ground state of a quantum system of identical bosons using the Hartree–Fock approximation and the pseudopotential interaction model. For time-discretization one can use either the first-order implicit Euler method or the second-order Crank-Nicolson method.
Problem description¶
The computational domain is the square 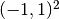 and boundary conditions are zero Dirichlet. The equation has the form
and boundary conditions are zero Dirichlet. The equation has the form
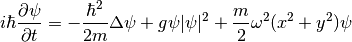
where 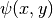 is the unknown solution (wave function),
is the unknown solution (wave function), 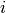 the complex unit,
the complex unit,
 the Planck constant,
the Planck constant, 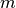 the mass of the boson,
the mass of the boson,
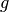 the coupling constant (proportional to the scattering length of two interacting bosons) and
the coupling constant (proportional to the scattering length of two interacting bosons) and
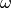 the frequency.
the frequency.