Basic-rk-newton¶
Model problem¶
This example is similar to basic-ie-newton except it uses the arbitrary Runge-Kutta methods in time.
We assume the time-dependent Richard’s equation
(1)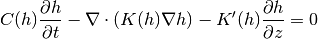
where 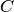 and
and 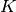 are given functions of the unknown pressure head
are given functions of the unknown pressure head 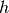 ,
,  are spatial coordinates, and
are spatial coordinates, and 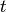 is time.
is time.
equipped with a Dirichlet, given by the initial condition.
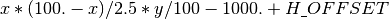
The pressure head ‘h’ is between -1000 and 0. For convenience, we increase it by an offset H_OFFSET = 1000. In this way we can start from a zero coefficient vector.
Defining weak forms¶
The weak formulation is a combination of custom Jacobian and Residual weak forms:
CustomWeakFormRichardsRK::CustomWeakFormRichardsRK() : WeakForm<double>(1)
{
// Jacobian volumetric part.
CustomJacobianFormVol* jac_form_vol = new CustomJacobianFormVol(0, 0);
add_matrix_form(jac_form_vol);
// Residual - volumetric.
CustomResidualFormVol* res_form_vol = new CustomResidualFormVol(0);
add_vector_form(res_form_vol);
}