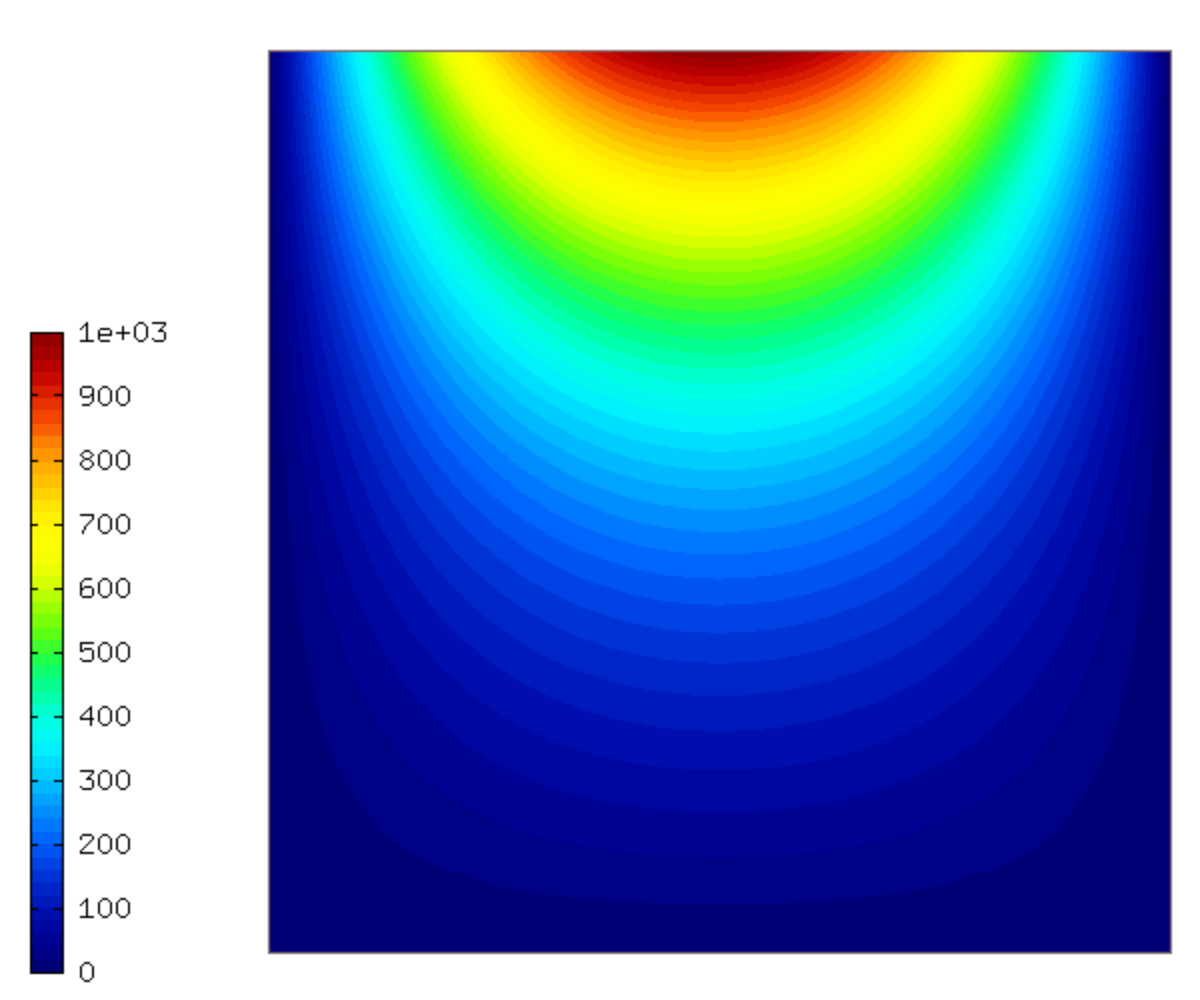
Basic-ie-picard¶
Model problem¶
This example is similar to basic-ie-newton except it uses the Picard’s method in each time step (not Newton’s method).
We assume the time-dependent Richard’s equation
(1)
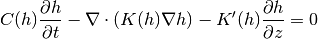
where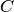 
and 
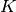are non-differentiable and thus in some cases the Newton’s method has convergence problems.
For this reason, the Picard’s method is a popular approach. If Picards is used, then Andersson acceleration should be employed.
equipped with a Dirichlet, given by the initial condition.
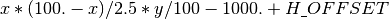
The pressure head ‘h’ is between -1000 and 0. For convenience, we increase it by an offset H_OFFSET = 1000. In this way we can start from a zero coefficient vector.
Weak formulation¶
The corresponding weak formulation reads
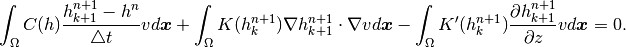
Here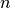 
refers to time steps and 
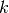to Picard’s iterations within one time step.
Defining weak forms¶
The weak formulation is a combination of custom Jacobian and Residual weak forms:
CustomWeakFormRichardsIEPicard::CustomWeakFormRichardsIEPicard(double time_step, Solution* h_time_prev, Solution* h_iter_prev) : WeakForm<double>(1)
{
// Jacobian.
CustomJacobian* matrix_form = new CustomJacobian(0, 0, time_step);
matrix_form->ext.push_back(h_time_prev);
matrix_form->ext.push_back(h_iter_prev);
add_matrix_form(matrix_form);
// Residual.
CustomResidual* vector_form = new CustomResidual(0, time_step);
vector_form->ext.push_back(h_time_prev);
vector_form->ext.push_back(h_iter_prev);
add_vector_form(vector_form);
}
