Microwave Oven¶
Problem description¶
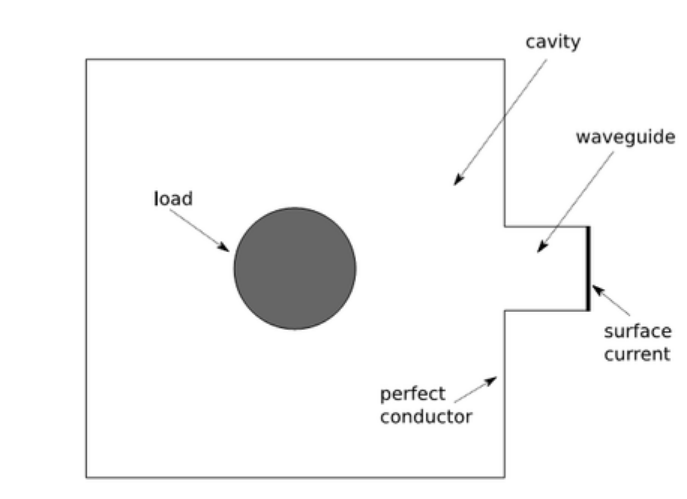
This example solves adaptively the electric field in a simplified microwave oven. The waves are generated using a harmonic surface current on the right-most edge. (Such small cavity is present in every microwave oven).
Equation solved: time-harmonic Maxwell’s equations.
Boundary conditions are perfect conductor on the boundary except for the right-most edge of the small cavity, where a harmonic surface current is prescribed.
Domain of interest: Square cavity with another small square cavity attached from outside on the right.
Material parameters¶
// Problem parameters.
const double e_0 = 8.8541878176 * 1e-12;
const double mu_0 = 1.256 * 1e-6;
const double e_r = 1.0;
const double mu_r = 1.0;
const double rho = 3820.0;
const double Cp = 7.531000;
const double freq = 1.0*2450000000.0;
const double omega = 2 * M_PI * freq;
const double c = 1 / sqrt(e_0 * mu_0);
const double kappa = 2 * M_PI * freq * sqrt(e_0 * mu_0);
const double J = 0.0000033333;
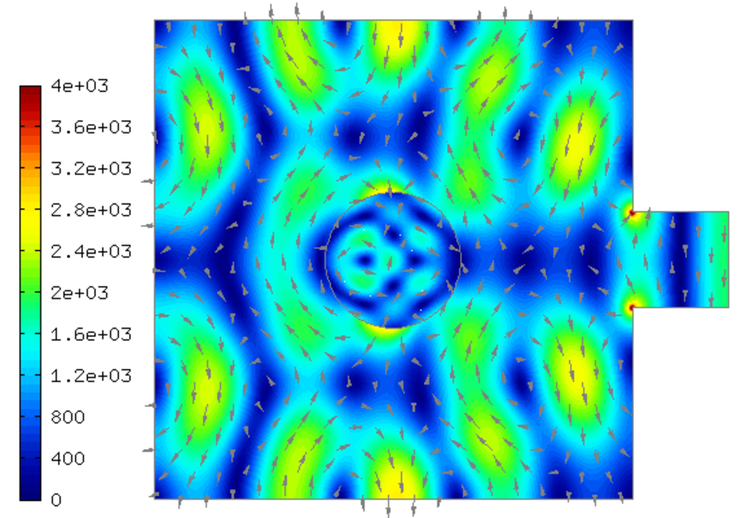
Sample solution¶
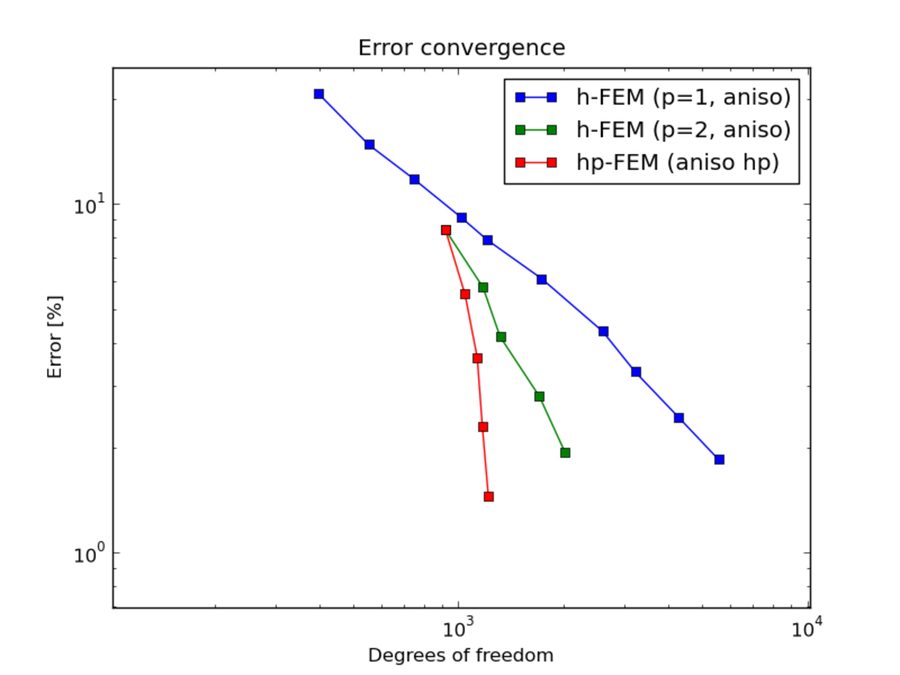
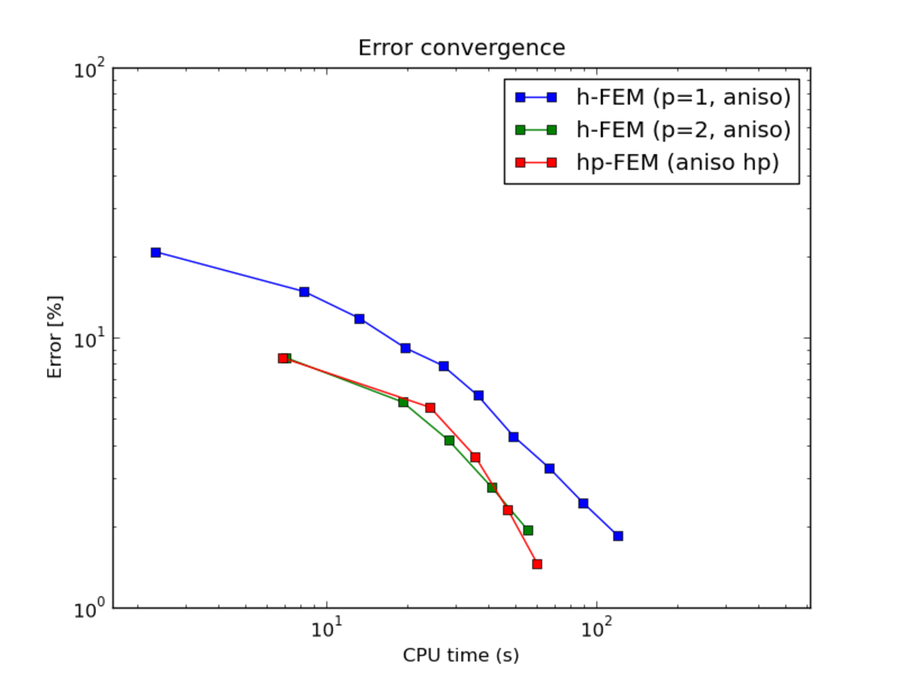
Comparison of h-FEM (p=1), h-FEM (p=2) and hp-FEM with anisotropic refinements¶
Final mesh (h-FEM, p=1, anisotropic refinements):
Final mesh (h-FEM, p=2, anisotropic refinements):
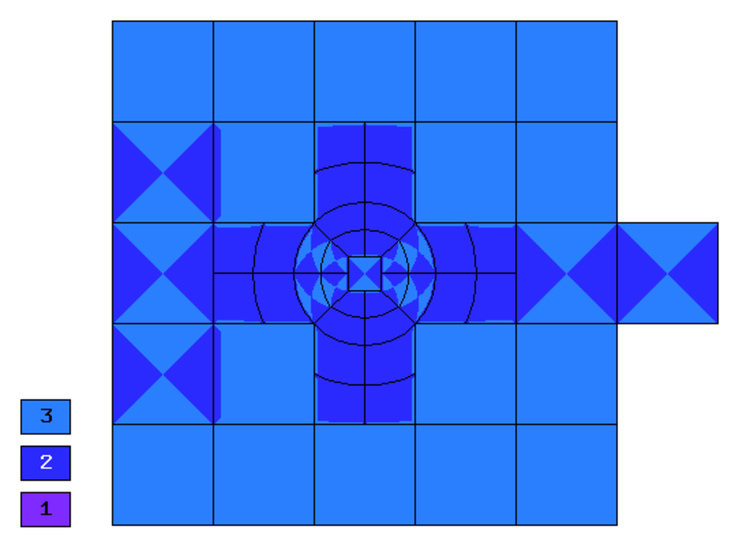
Final mesh (hp-FEM, h-anisotropic refinements):
DOF convergence graphs:
CPU convergence graphs: