Apartment¶

Problem description¶

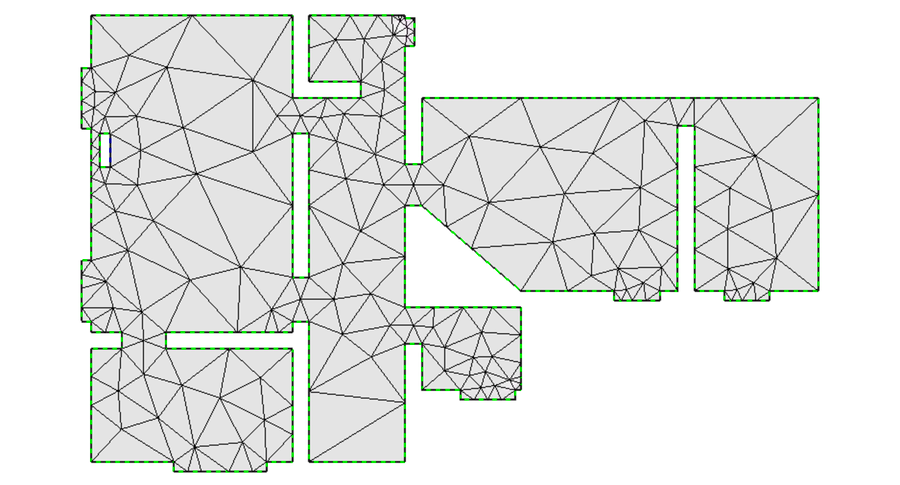
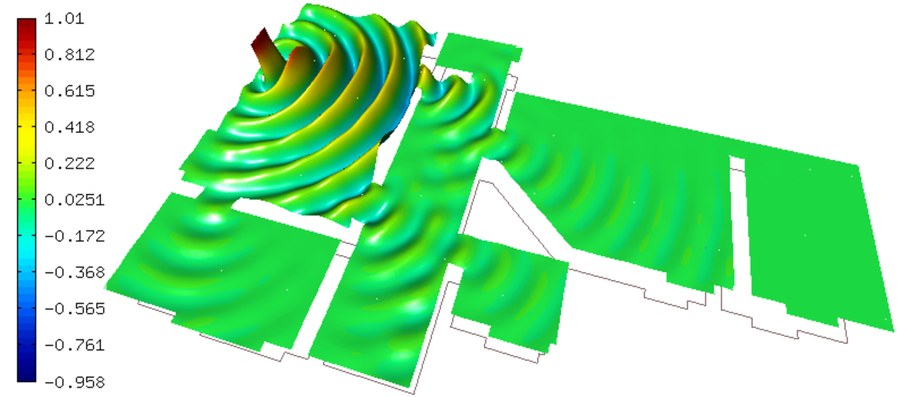
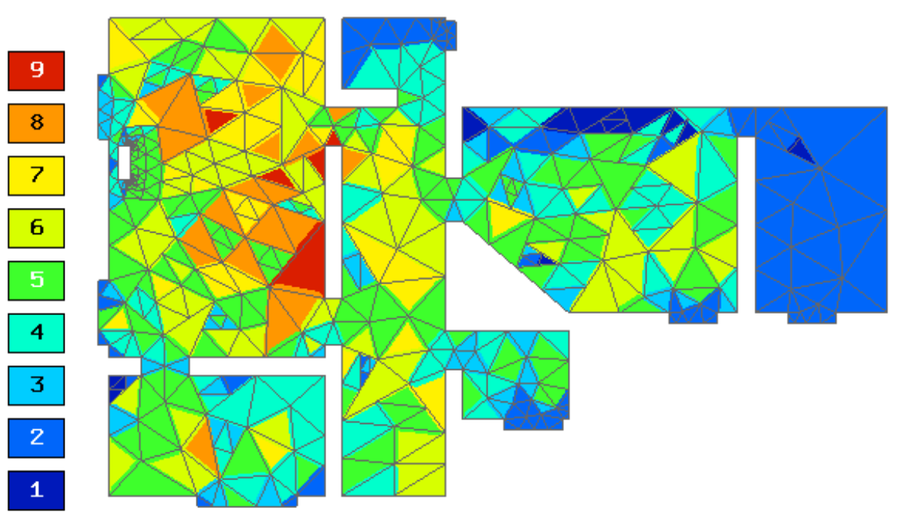
This example solves adaptively the pressure field in an apartment, that is caused by a harmonic local acoustics source. The geometry and initial mesh are shown below.

Equation solved:

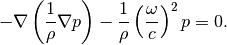
$-\nabla \left(\frac{1}{\rho} \nabla p\right) - \frac{1}{\rho}\left(\frac{\omega}{c}\right)^2 p = 0.$

Boundary conditions are Dirichlet (prescribed pressure) on one edge. The rest of the boundary are wall with a Newton condition (matched boundary).

$\frac{1}{\rho} \frac{\partial p}{\partial n} = \frac{j \omega p}{\rho c}$

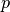Here $p$ is pressure, 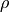$\rho$ density of air, $\omega = 2 \pi f$ angular frequency, and $c$ speed of sound. See the main.cpp file for concrete values.

Sample results¶

Pressure distribution:

Final mesh:

Apartment¶

Problem description¶

Sample results¶

Table Of Contents

Previous topic

Next topic

Navigation

Apartment¶

Problem description¶

Sample results¶

Table Of Contents

Previous topic

Next topic

Quick search

Navigation