NIST-11 (Intersecting Interfaces)¶
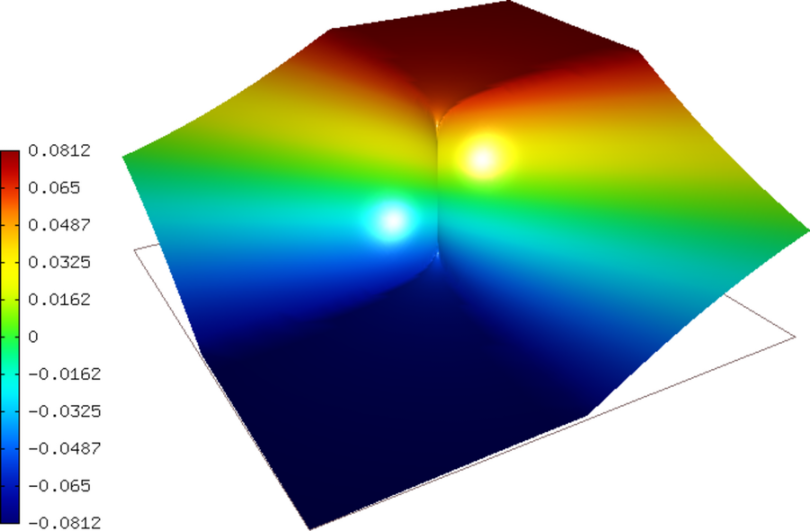
The solution to this problem has a discontinuous derivative along the interfaces, and an infinite derivative at the origin that posses a challenge to adaptive algorithms.
Model problem¶
Equation solved:
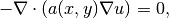
Parameter  is piecewise constant,
is piecewise constant, 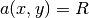 in the first and third quadrants, and
in the first and third quadrants, and 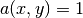 in the remaining two quadrants.
in the remaining two quadrants.
Domain of interest: 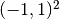 .
.
Boundary conditions: Dirichlet, given by exact solution.
Exact solution¶
Quite complicated, see the source code.
Sample solution¶
Comparison of h-FEM (p=1), h-FEM (p=2) and hp-FEM with anisotropic refinements¶
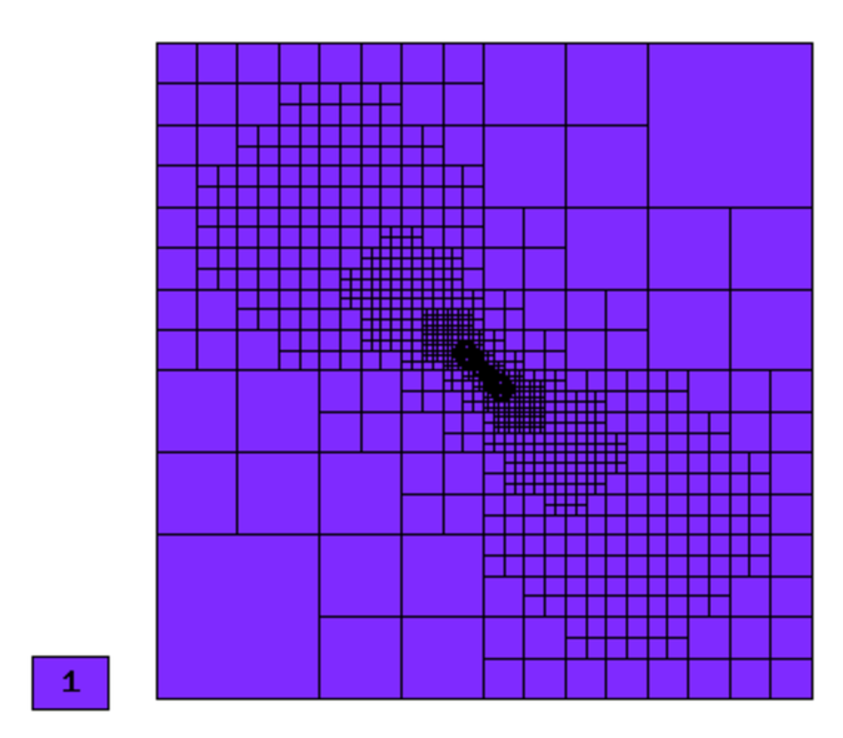
Final mesh (h-FEM, p=1, anisotropic refinements):
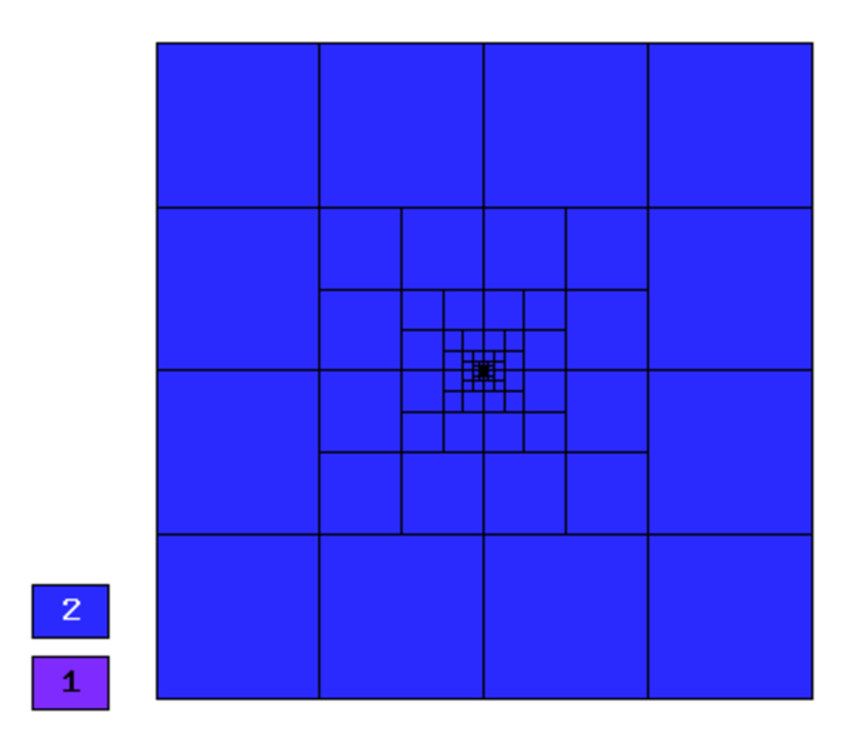
Final mesh (h-FEM, p=2, anisotropic refinements):
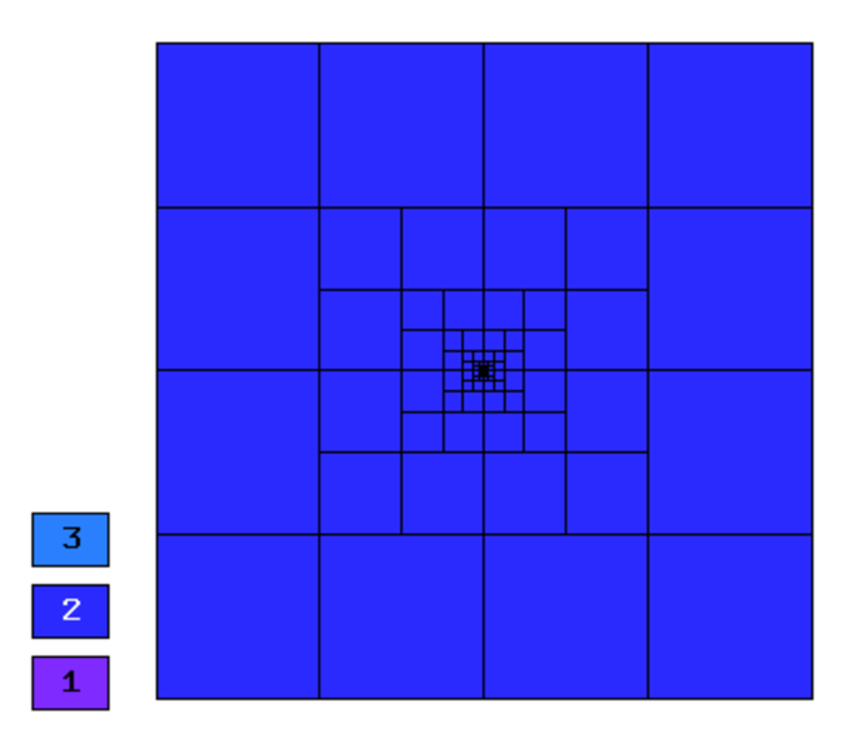
Final mesh (hp-FEM, h-anisotropic refinements):
DOF convergence graphs:
CPU convergence graphs: