NIST-05 (Battery):¶
Model problem¶
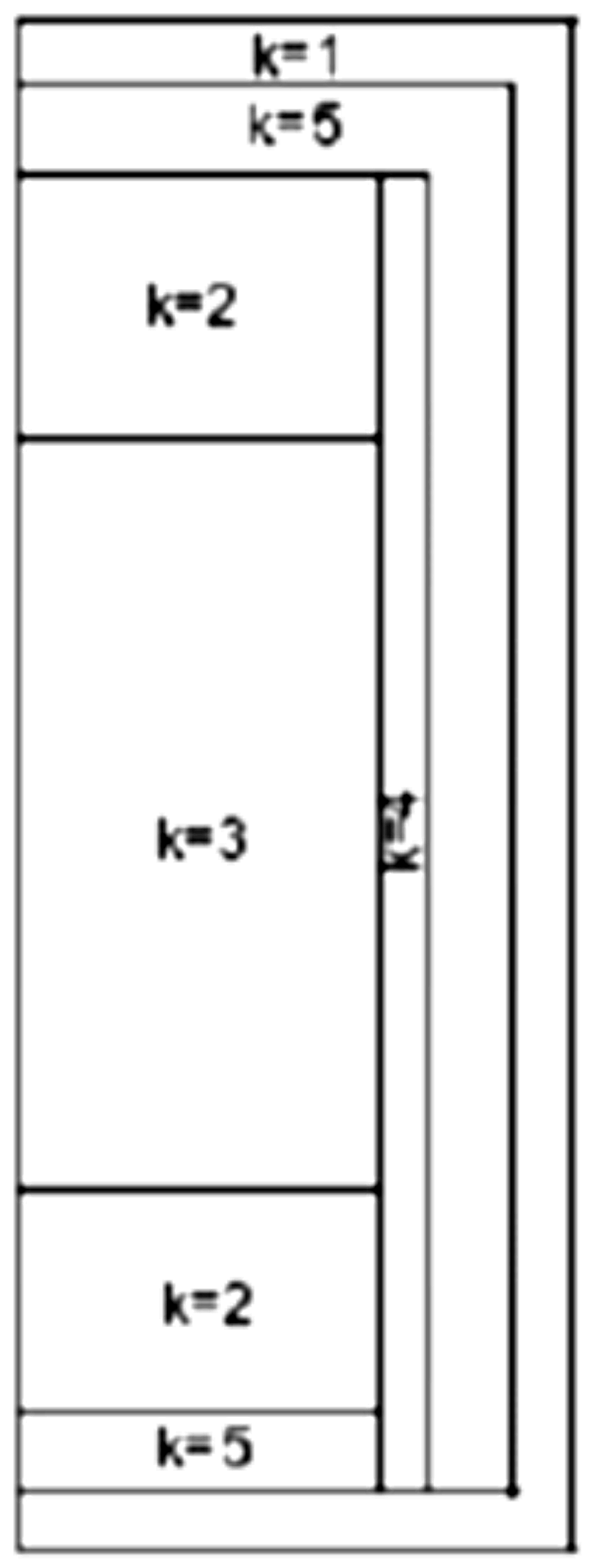
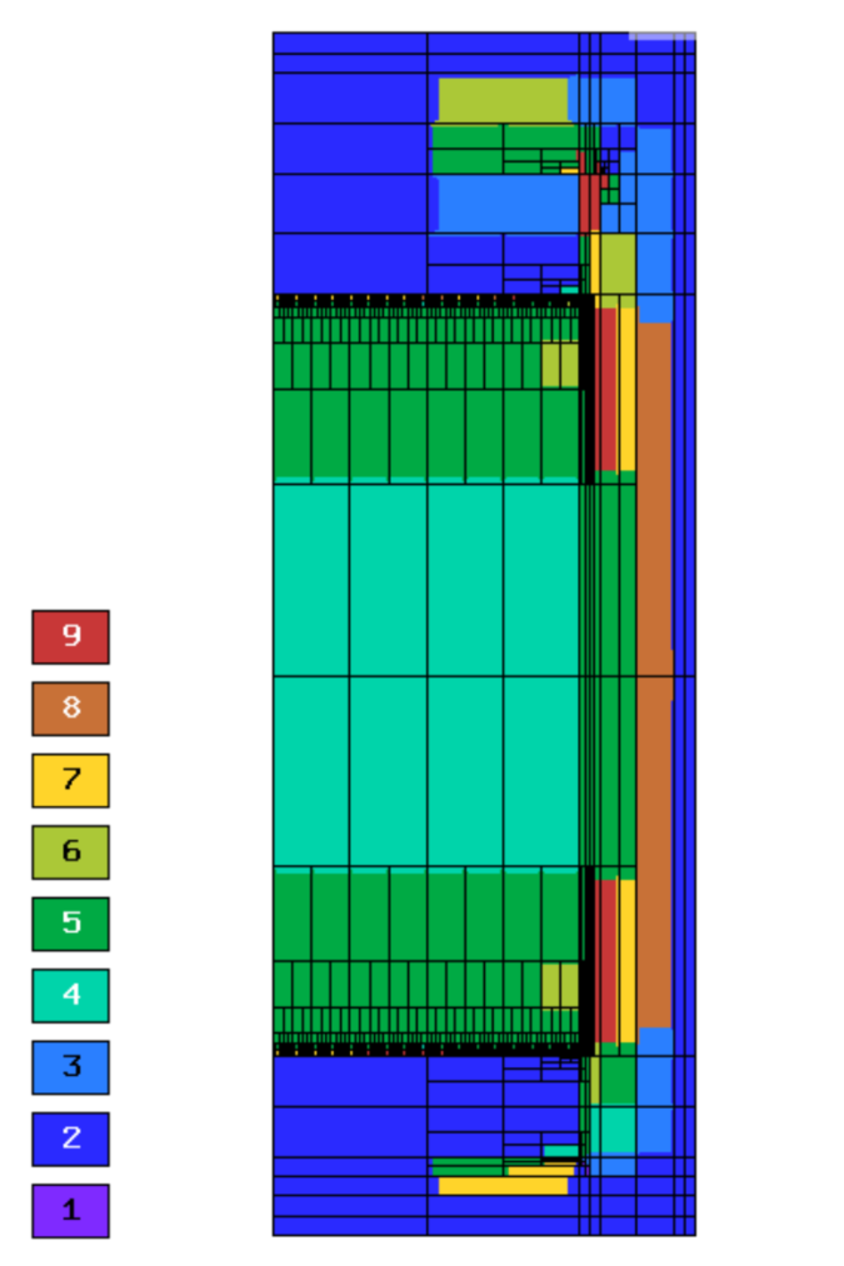
This problem models heat conduction in a battery with nonhomogeneous materials. The solution has multiple point singularities in the interior of the domain. The domain is the rectangle shown in the following figure; the numbered regions indicate the areas of different material constants.
Equation solved:
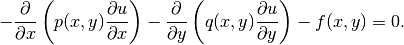
Boundary conditions: Zero Neumann on left edge, and Newton on the rest of the boundary:
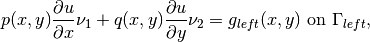
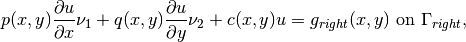

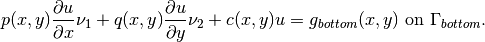
Here 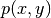 ,
, 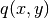 , and the right hand side
, and the right hand side 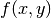 are constant coefficient functions in different materials.
are constant coefficient functions in different materials.
Domain of interest: 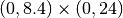 .
.
Exact solution: Unknown.
Material parameters¶
// Problem parameters.
const int OMEGA_1 = 1;
const int OMEGA_2 = 2;
const int OMEGA_3 = 3;
const int OMEGA_4 = 4;
const int OMEGA_5 = 5;
const double P_1 = 25.0;
const double P_2 = 7.0;
const double P_3 = 5.0;
const double P_4 = 0.2;
const double P_5 = 0.05;
const double Q_1 = 25.0;
const double Q_2 = 0.8;
const double Q_3 = 0.0001;
const double Q_4 = 0.2;
const double Q_5 = 0.05;
const double F_1 = 0.0;
const double F_2 = 1.0;
const double F_3 = 1.0;
const double F_4 = 0.0;
const double F_5 = 0.0;
Boundary condition parameters¶
// Boundary condition coefficients for the four sides.
const double C_LEFT = 0.0;
const double C_TOP = 1.0;
const double C_RIGHT = 2.0;
const double C_BOTTOM = 3.0;
const double G_N_LEFT = 0.0;
const double G_N_TOP = 3.0;
const double G_N_RIGHT = 2.0;
const double G_N_BOTTOM = 1.0;
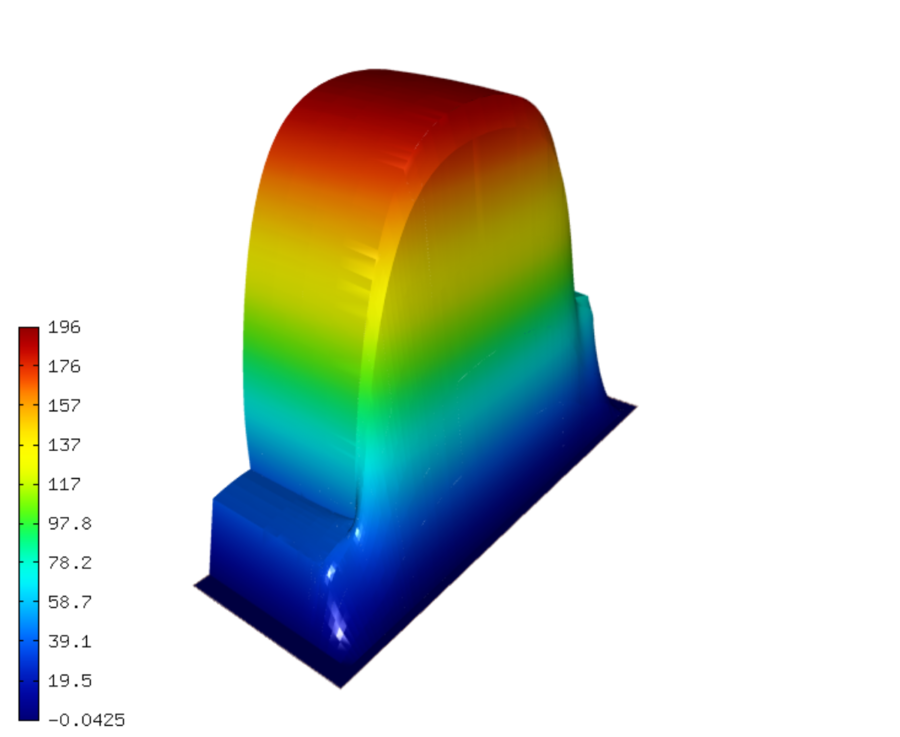
Sample solution¶
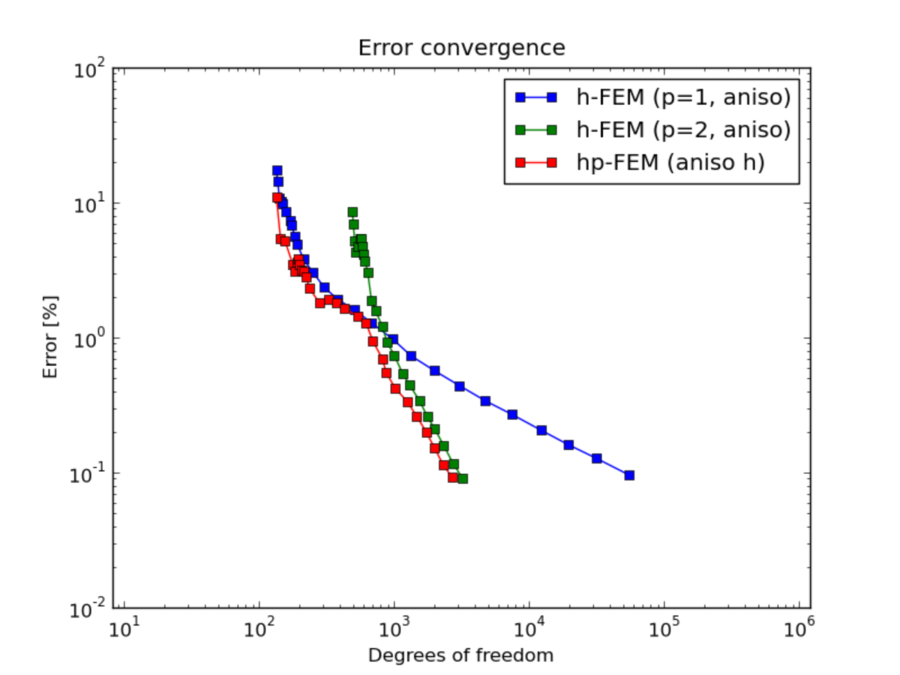
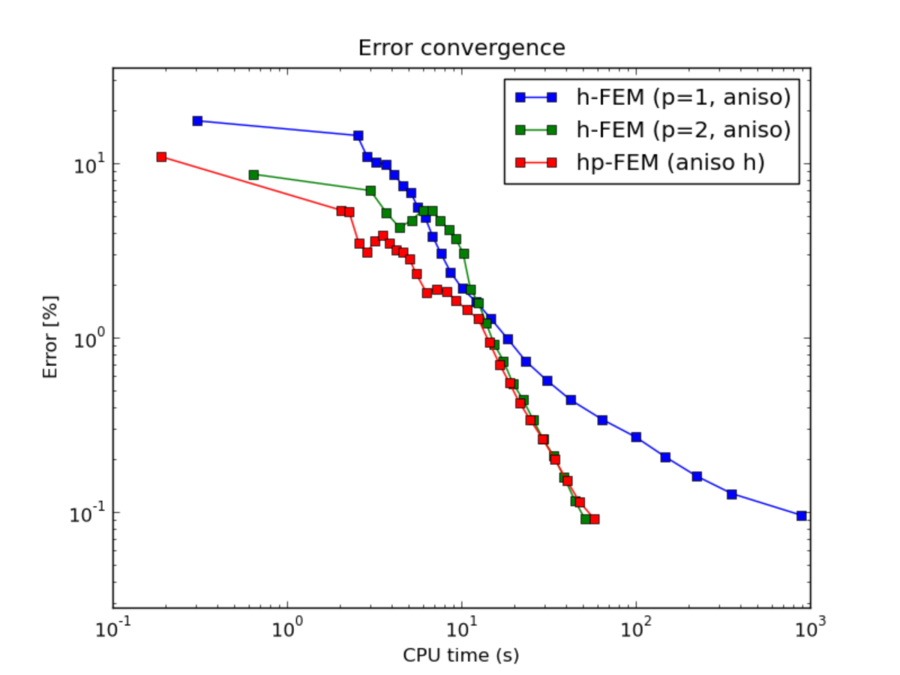
Comparison of h-FEM (p=1), h-FEM (p=2) and hp-FEM with anisotropic refinements¶
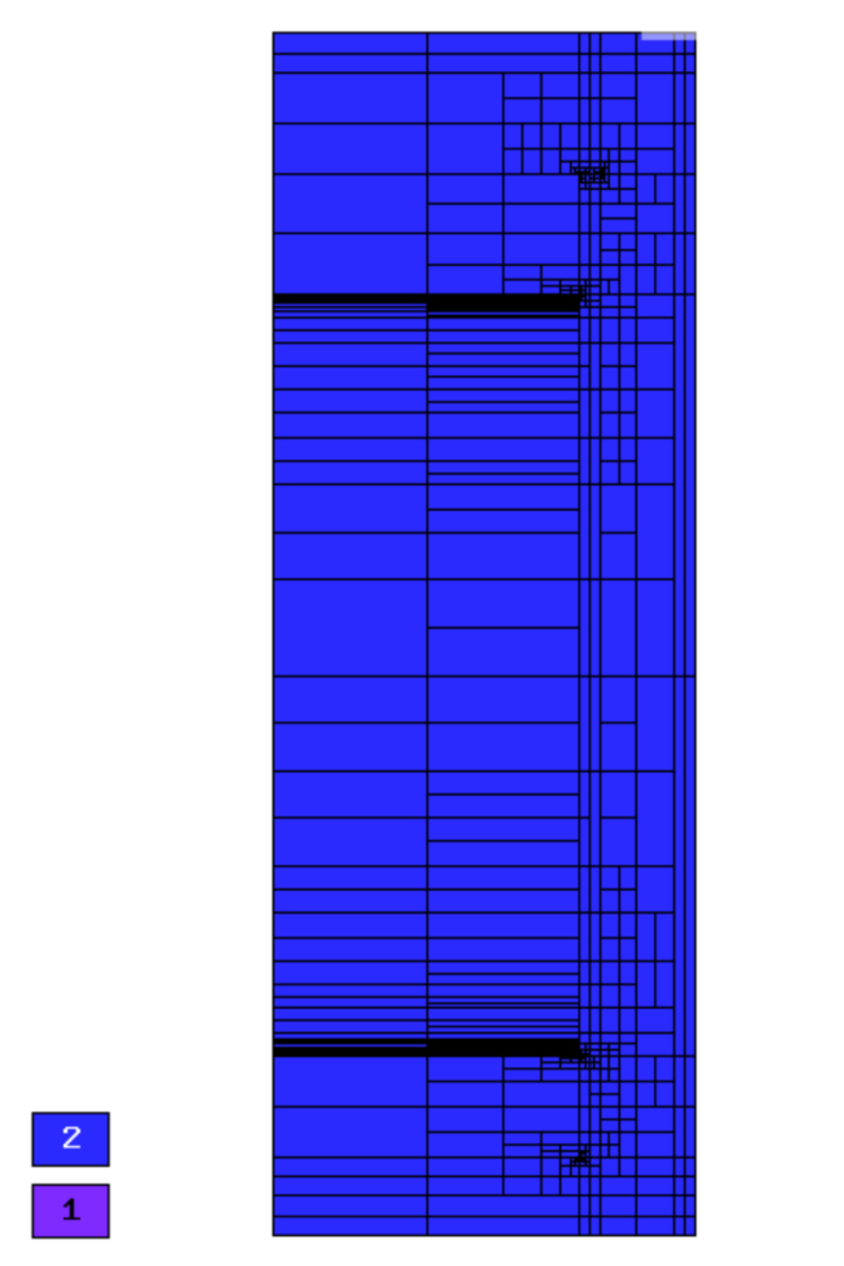
Final mesh (h-FEM, p=1, anisotropic refinements):
Final mesh (h-FEM, p=2, anisotropic refinements):
Final mesh (hp-FEM, h-anisotropic refinements):
DOF convergence graphs:
CPU convergence graphs:
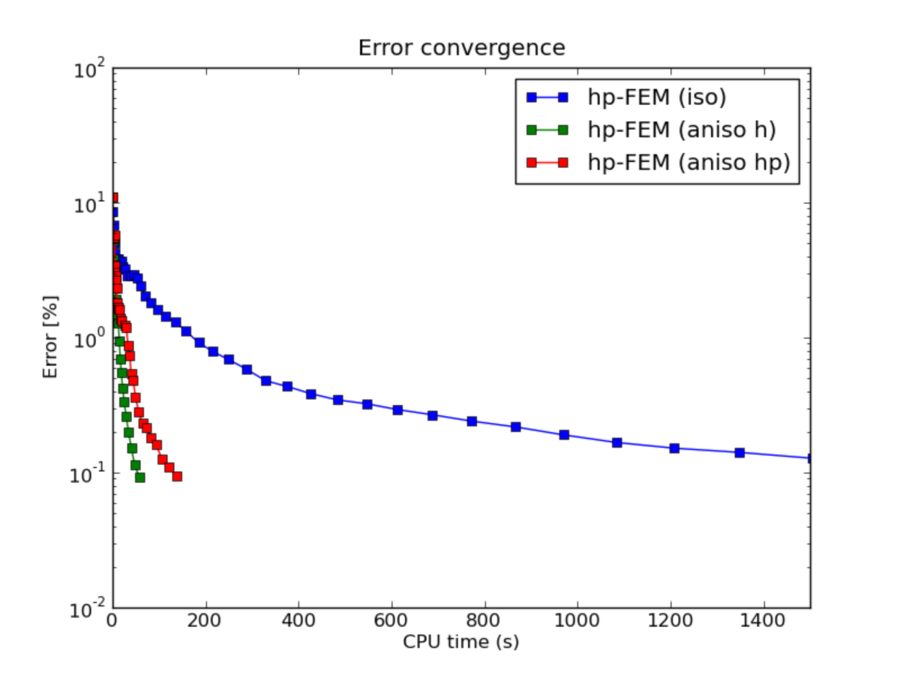
hp-FEM with iso, h-aniso and hp-aniso refinements¶
Final mesh (hp-FEM, isotropic refinements):
Final mesh (hp-FEM, h-anisotropic refinements):
Final mesh (hp-FEM, hp-anisotropic refinements):
DOF convergence graphs:
CPU convergence graphs: