Screen (Maxwell’s Equations)¶
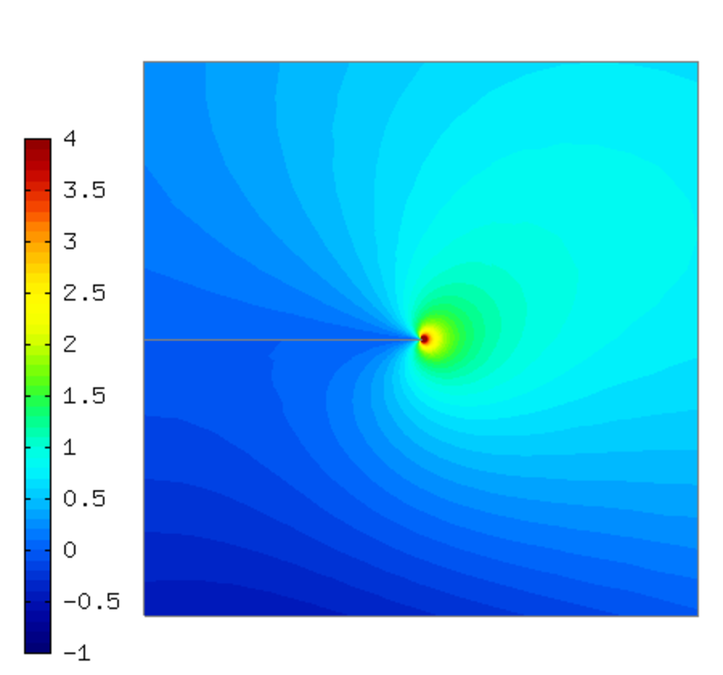
This example solves time-harmonic Maxwell’s equations. It describes an electromagnetic wave that hits a thin screen under the angle of 45 degrees, causing a singularity at the tip of the screen. The strength of the singularity makes this example rather difficult.
Model problem¶
Equation solved: Time-harmonic Maxwell’s equations
(1)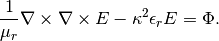
Domain of interest is the square 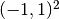 missing the edge that connects the center with
the midpoint of the left side. It is filled with air:
missing the edge that connects the center with
the midpoint of the left side. It is filled with air:
Boundary conditions¶
Tangential component of solution taken from known exact solution (essential BC).
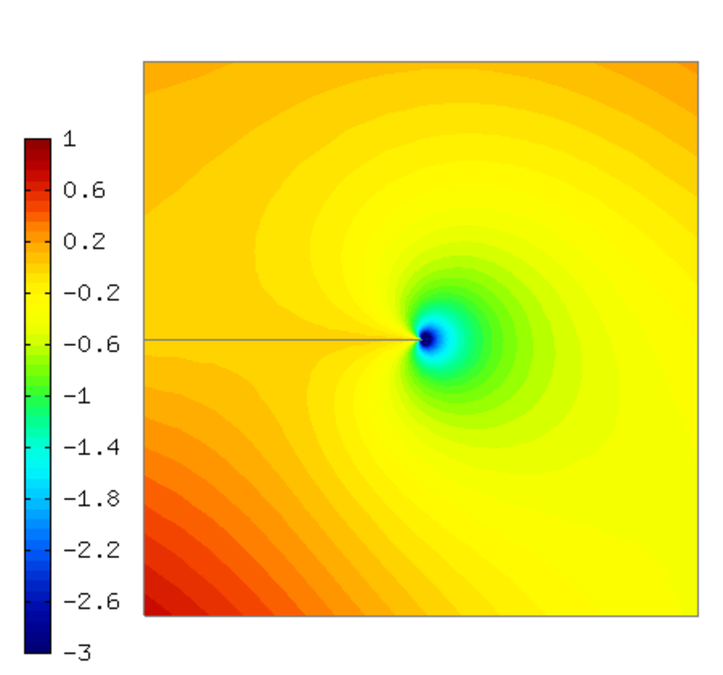
Exact solution¶
This is rather complicated in this case - see the file definitions.cpp.
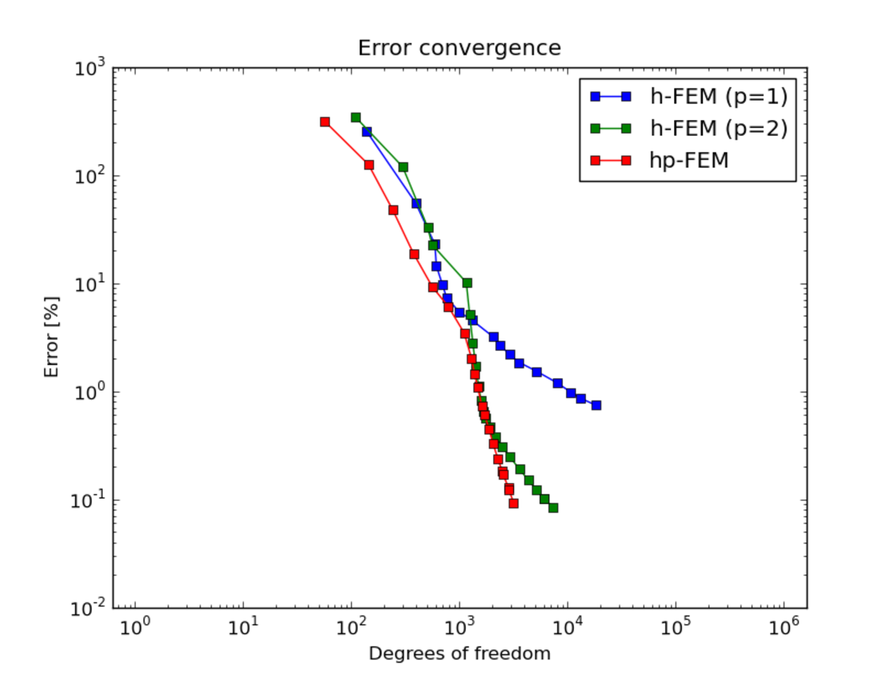
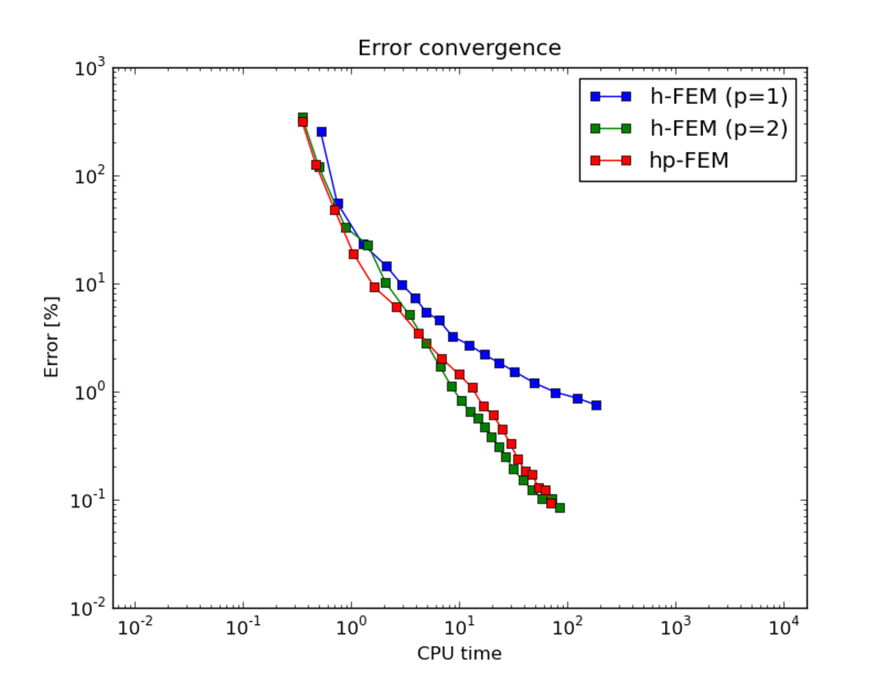
Convergence comparisons¶
Final mesh (h-FEM with linear elements):
Note that the polynomial order indicated corresponds to the tangential components of approximation on element interfaces, not to polynomial degrees inside the elements (those are one higher).
Final mesh (h-FEM with quadratic elements):
Final mesh (hp-FEM):
DOF convergence graphs:
CPU time convergence graphs:
 :
:
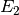 :
: